网络首发论文推荐|钢板混凝土组合剪力墙轴心受压模拟与栓钉抗剪的数值参数研究

土木交通工程大学、广州工程学院

概括

目前，厚板混凝土组合弯矩墙的研究主要集中在抗震性能方面，对其轴压性能和连接件拱圈受力特性的研究较少，更缺乏不同参数下翼缘板受力特性的研究。 纵梁充当剪力连接器，使板和混凝土能够协同工作，以最大限度地提高两者的性能。 然而，试验中很难测量纵梁的受力机制。 针对该问题，根据前人的试验研究数据，进一步研究了不同参数下厚板组合弯矩墙的极限承载力及纵梁剪力机理。 在前期厚板混凝土组合墙轴压试验的基础上，利用ABAQUS软件构建厚板混凝土组合弯矩墙有限元模型，并进行大范围变参数分析，研究不同参数下拱圈的受力分析和极限承载力。

有限元模型中混凝土、钢板、纵梁均采用C3D8R实体进行模拟，建立细化模型。 混凝土本构关系模型选用ABAQUS软件提供的混凝土塑性损伤模型； 钢与纵梁的本构关系采用二折线模型。 该模型不包括上、下端板，而是采用“刚体”约束对加载板进行建模，构造两个参考点（RP），两个参考点分别位于上、下横截面的中心，为两个RP赋予边界条件，在RP上方向下施加载荷。 板的上下表面和混凝土核心在所有自由度上都是固定的，而不仅仅是下端的位移。 接触方面：主要预制构件之间采用一般接触，法线方向为硬接触行为。 对于切向接触行为，本研究中的摩擦系数 μ 为 0.6。 为了防止剪切锁定，所有零件均采用扫掠网格定义技术，将组装好的零件划分为规则形状，然后输入种子数量，进行人工种子定义，得到正多面体。 其中，厚板的长度需要人工划分为宽度两层，一些不规则的网格也需要人工划分为规则的划分。 开口的位置被定义为四个网格。 最终划分形状后定义的网格具有更好的估计进度和效率。 通过模拟试件中厚板的屈曲变形，验证了有限元建模过程的合理性和分析结果的可靠性，完善了13个有限元变参数模型，研究了不同参数下试件的极限承载力和纵梁受剪受力机理。

参数分析结果表明：所选本构关系、接触关系和边界条件等有限元参数能够模拟厚板混凝土组合弯矩墙的位移加载和破坏过程，荷载-位移曲线和厚板屈曲规律与试验结果一致； 长高比L/H、混凝土硬度和钢材硬度对试件极限承载力影响较大，且影响基本呈线性关系。 强混凝土与拱圈的协同作用更强； 拱圈的挠度集中在内侧，当板的硬度与纵梁的硬度一致时，拱圈的内侧挠度可以达到较大的值，拱圈的抗剪性能可以充分发挥，与混凝土的协同作用更强。

厚板组合弯矩墙由两块厚板和中间填充混凝土组成。 国外学者对厚板组合弯矩墙的静力性能和抗震性能进行了试验研究和数值分析，结果表明混凝土与厚板连接件（如纵梁、拉力螺钉和伸臂肋等）可以有效提高厚板的稳定承载力。 厚板复合弯矩墙早已应用于南京高银117大厦、核电站等复杂结构。

但目前的研究主要集中在厚板组合弯矩墙的抗震性能方面，对其轴压性能和连接件拱圈受力特性的研究较少，更缺乏对不同参数下翼缘板受力特性的研究。 拱圈作为剪力缝，使厚板和混凝土共同作用，最大限度地发挥两者的性能，但试验中很难测量拱圈的受力机制。 为了解决这个问题，根据张友佳等人的试验结果。 结合相关文献的有限元模拟结果，本文利用ABAQUS软件构建了轴压工况下厚板组合弯矩墙的有限元模型，对有限元模拟结果进行修正，并进行广泛的变参数分析，研究不同参数下拱圈的受力分析和极限承载力，为工程设计提出建议。 因此，本文对长高比、混凝土硬度、钢板硬度和纵梁硬度等多个参数进行分析，研究各参数下纵梁的受力特性。

1 测试概述

为了验证有限元模型的有效性和合理性，对文献报道的厚板混凝土组合墙轴压试验进行了模拟。 有4个测试样本。 试件规格及式样见图1，加载装置见图2。材料试验见表1，试验结果见表2。混凝土六面体抗压硬度为32.6MPa。

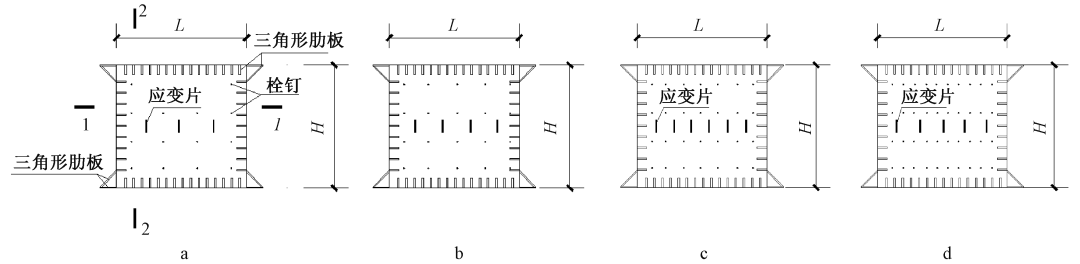
a—SCW-1； b—SCW-2； c—SCW-3； d—SCW-4。

图 1 样本规格

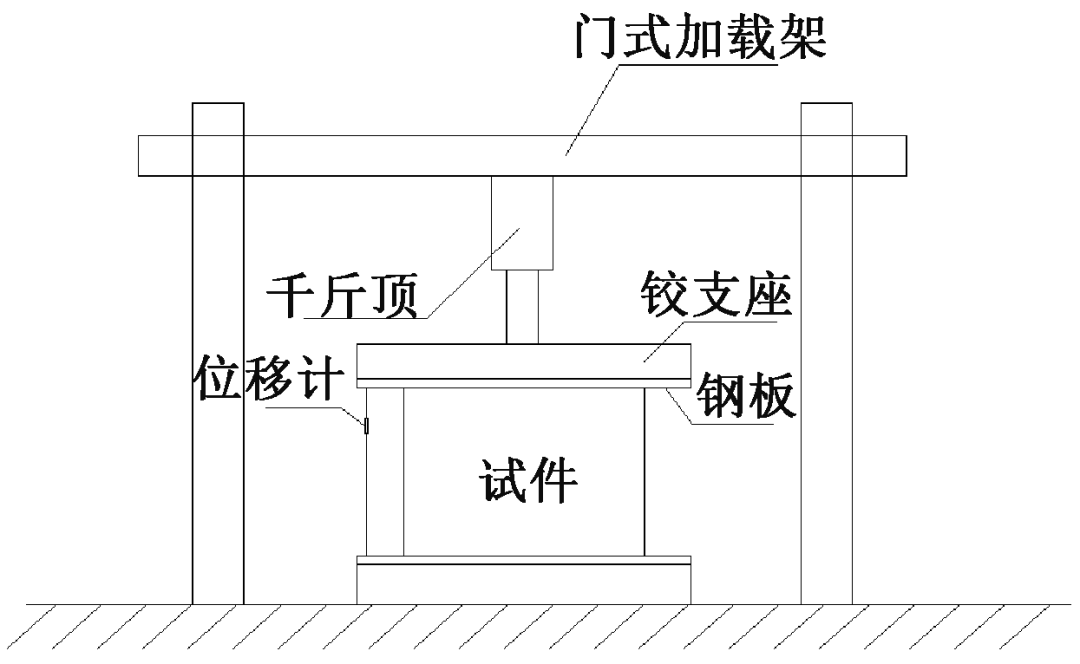
图2 加载装置

表1 材料性能测试结果 MPa

注：fy表示钢的屈服硬度； fu表示钢的极限延伸硬度。

表2 预制构件承载力测试

注：距厚比是指拱圈宽度与厚板长度之比。

2 有限元分析

首先，对厚板混凝土组合弯矩墙的有限元模型进行了模拟。 通过将位移-极限载荷和厚板屈曲模拟与文献中的实验结果进行比较，验证了有限元模型。 验证有限元建模的合理性和结果的可靠性后，对不同参数下的拱圈进行受力研究，包括长高比L/H、混凝土硬度、钢板硬度和纵梁硬度。

2.1 有限元模型描述

有限元模型是使用ABAQUS有限元软件开发的。 据记载，初始缺陷和残余变形仅对空心预制构件的性能产生显着影响。 对于厚板混凝土组合弯矩墙，局部缺陷和残余变形的影响可以通过混凝土填充最小化，因此在当前的有限元模拟中被忽略。 陶忠等人的研究也否定了这一点。

2.1.1 几何和网格

核心混凝土、钢板和纵梁采用实体 8 节点简化集成 C3D8R 单元进行建模。 据悉，值得强调的是，进行了网格敏感性分析，以找到合适的网格尺寸。 现有文献强调，合理的网格密度是两种不同网格密度的分析结果差异不超过5%，并且有合理的估计时间。 因此，板和螺杆网格定义为20mm，为了提高估算效率，混凝土实体单元网格定义为40mm。 网格均通过ABAQUS中的扫掠网格技术定义，如图3所示。将板和纵梁组合为第1部分，将混凝土组合为第2部分，并将每个部分划分为规则的形状。

a——具体网格定义； b——钢格板定义； c——螺旋网格定义。

图3 网格定义

2.1.2 混凝土本构关系模型

混凝土本构模型主要是指混凝土材料在多轴挠曲状态下的挠度-应变关系。 为了更好地模拟约束混凝土的力学性能，选用ABAQUS软件提供的混凝土塑性损伤模型作为混凝土的本构模型。 该模型可以准确模拟混凝土的两种主要破坏模式，即拉伸破坏和压缩破碎破坏。 Lubliner 等人提出的屈服面。 和李等人。 以及 Hillerborg 等人提出的断裂能准则。 被采用。 屈服挠度取2.49，断裂能取0.08。

在模型的参数设置中，所选的塑性损伤模型采用非关联流定律，塑性势面函数中的混凝土展开角设置为38°，偏心率设置为0.1； 控制混凝土屈服面的双轴极限抗压硬度与单轴极限抗压硬度之比σb0/σc0设定为1.16； 控制混凝土屈服面在局部平面上的投影形状的参数K设定为2/3； 为了提高模型在软化阶段的收敛速度，选择粘度参数为1.0×10-5。 混凝土的弹性挠度根据ACI提供的公式估算：

式中：f'c为混凝土锥体的抗压硬度。

混凝土模量取0.2。 对厚板混凝土结构施加竖向荷载，由于内填充混凝土的纵向变形受到两侧厚板的约束，使其在三维压缩下处于挠曲状态，热工性能大大提高。 因此，林海汉等人给出的具体本构关系。 损伤因子采用李伟提出的公式。

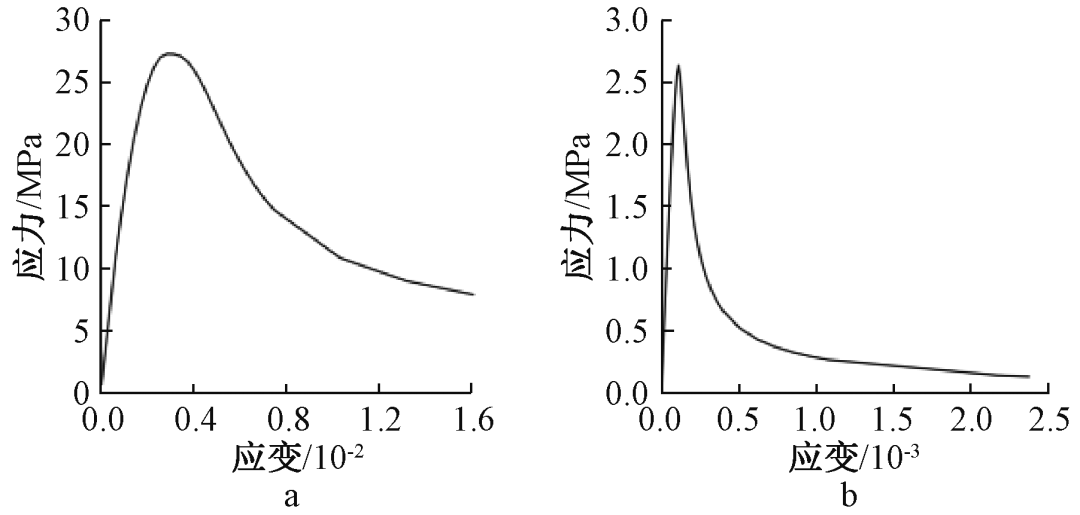
a——在压力下； b——在张力下。

图4 混凝土挠度-应变曲线

2.1.3 钢材本构关系模型

采用ABAQUS的各向同性弹塑性模型来模拟钢材的应力。 钢材单轴挠度-应变关系取自法国规范EC3提出的双折线模型，弹性截面斜率为弹性挠度E=2.06×105MPa，加强截面斜率为0.01E。 如图5所示，其中σ和ε分别为钢材的挠度和应变，εy为屈服拉伸应变，fy为屈服硬度，εu为极限拉伸应变，fu为伸长硬度，模量为0.3。 厚板的硬度等级如表3所示。

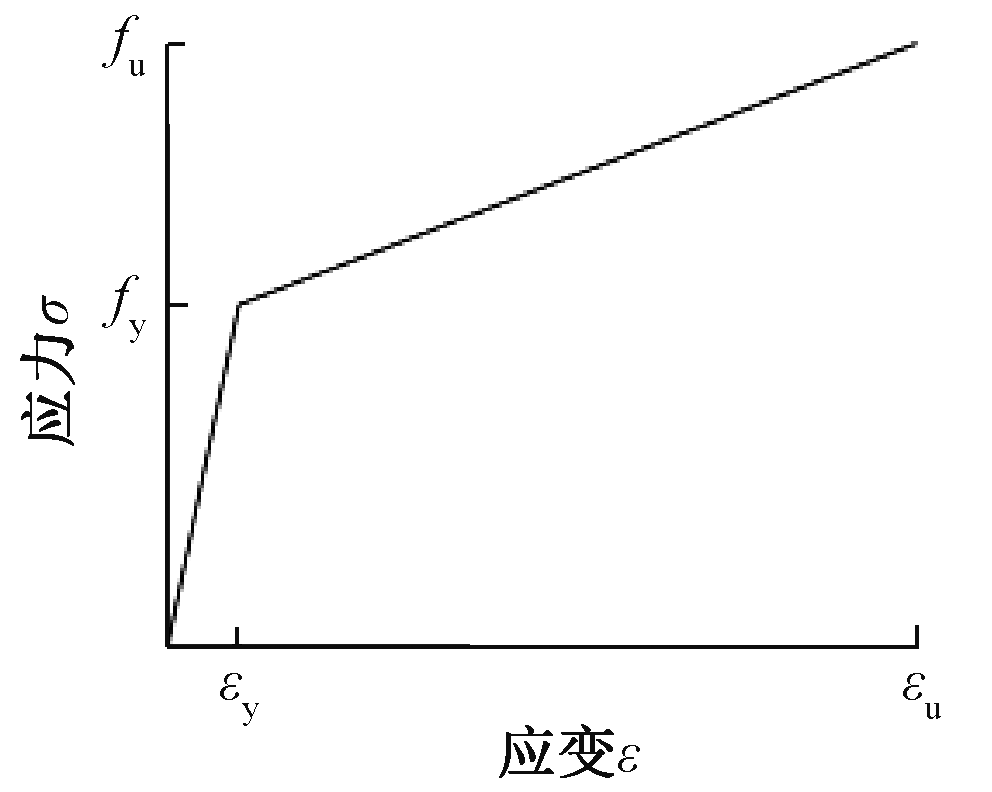
图5 钢材单轴挠度-应变关系曲线

表3 有限元模型试验数据与极限载荷对比

2.1.4 边界条件和相互作用

有限元模型如图6所示。该模型不包括上下端板，而是使用“刚体”约束对加载板进行建模。 两个参考点（RP）位于上、下横截面的中心。 边界条件分配给两个 RP，同时在 RP 上方向下施加载荷。 板的上下表面和混凝土核心在所有自由度上都是固定的，而不仅仅是下端的位移。 这是陶忠等人发现的。 该方法可以模拟端板。 随后丁等人也予以否认。

另外，混凝土核心筒（第2部分）与板纵梁（第1部分）之间的相互作用采用一般接触，法线方向为硬接触行为，对于切向接触行为，本研究采用摩擦系数μ为0.6。

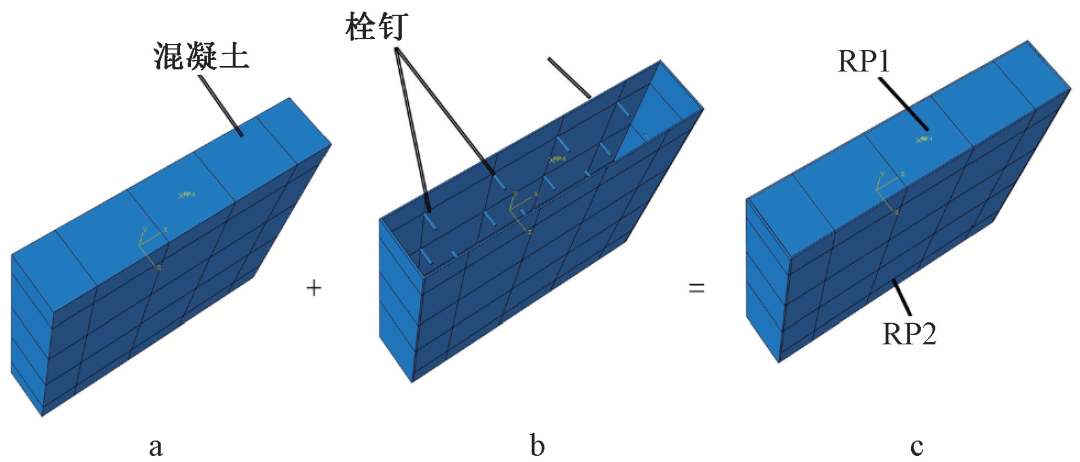
a——第1部分； b——第2部分； c——整体。

图6 有限元几何模型

2.2 有限元模型验证

试件有限元估算结果与试验结果的位移-载荷曲线对比如图7所示。可以看出，有限元试件的峰值载荷与试验吻合较好，且SCW-1和SCW-3的有限元位移载荷基本小于试验载荷值，因为有限元试件处于理想状态。 相关文献表明，SCW-4试件在加载后期出现失稳破坏，导致其有限元模拟值大于试验值，且载荷快速增加，因此在成长期三者并不一致。 在弹力范围内，所有试件的初始挠度也吻合较好，能够更好地模拟试件的初始挠度。 综上所述，本文的有限元模型能够较好地模拟厚板组合弯矩墙的轴压性能。 另外，从有限元模型与试验数据的对比（表3）还可以发现，有限元值Nu，FEA与试验极限载荷Nu，exp吻合较好。

a——SCW-1样本； b——SCW-3试样； c—SCW-4 样本。

图7 试验值与有限元模拟值的应变-载荷关系曲线

2.3 模拟屈曲

本文通过有限元建模，以U1（单元节点在x轴上的位移）来反映厚板的局部屈曲。 厚板屈曲的实验现象取自文献。 从图8可以看出，ABAQUS模拟估算的厚板屈曲位置与实验观察基本一致，再次证明本文构建的有限元模型能够准确模拟厚板组合弯矩墙的力学性能。

SCW-1和SCW-3试验中，中间厚板表现出典型的屈曲。 在有限元中可以看出，屈曲也发生在有限元试件的中部，这与试验一致。 SCW-1的最大位移为21.95mm，SCW-3的最大位移为17.80mm。

试验过程中，SCW-4因加载后期出现局部塌陷，试验现象不明显，有限元模拟较困难。 有限元分析中可以看出，SCW-4试件的最大位移为2.77mm，且均匀分布在中部。 板与混凝土的位移差为1.02mm，即有限元中板不发生屈曲，与实验现象一致。 可见，当冠梁宽度较小时，可以保证厚板与混凝土的协调工作。

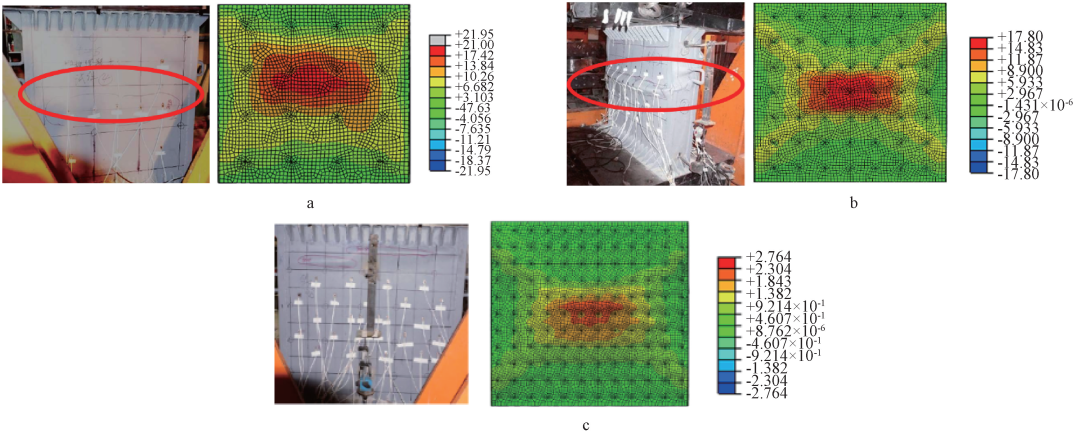
a——SCW-1中厚板U1方向位移及截面； b——SCW-3中厚板U1方向位移及截面； c—SCW-4中厚板U1方向位移及剖面。

图8 厚板屈曲模拟

3 参数分析

基于上述有限元模型的参数设置，本文分析了所有变参数研究的结果，但分析了13个模拟模型的极限载荷和纵梁应力特征，数值总结如表4。

表4 变参数研究结果

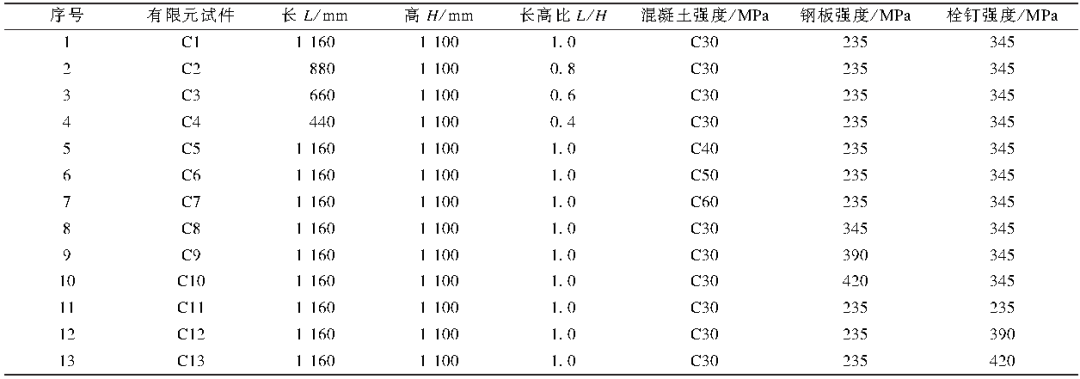
注：相关文献表明，当距厚比小于60时，试件容易出现局部失稳。 因此，本文的变参数模型假设纵梁距厚比为31，外壁厚板长度为5 mm，右厚板长度为8 mm，试件长度为230 mm。

3.1 纵横比

通过改变厚板组合抗弯墙的厚度L，论证了不同长高比L/H对单层厚板组合抗弯墙轴压极限承载力的影响，以及不同长高比L/H下纵梁的应力。 从图9a可以看出，在相同材料硬度下，组合弯矩壁的轴向压缩载荷-位移曲线随着L/H的减小而减小，且几乎呈线性减小。 当L/H=1较大时，峰值载荷后预制构件的承载能力大幅增加，且容易形成延性破坏，这可以表明较小的长径比可以适当改善预制构件的脆性。 另外，从有限元试件的挠度云图（图9b、c、e、f）可以看出，不同长高比的试件均呈现出统一规律，即纵梁内侧挠度较大。 可见，作为柔性剪力节点，纵梁内侧的剪力阻力是其主要受力模式。

由图9e和图9f可知，对于C4试件（长高比较小），中纵梁内侧最大挠度几乎接近厚板最大挠度，最大挠度可达238.5MPa。 表明长高比越小，板与混凝土的配合能力越强，纵梁传递的弯矩越大。

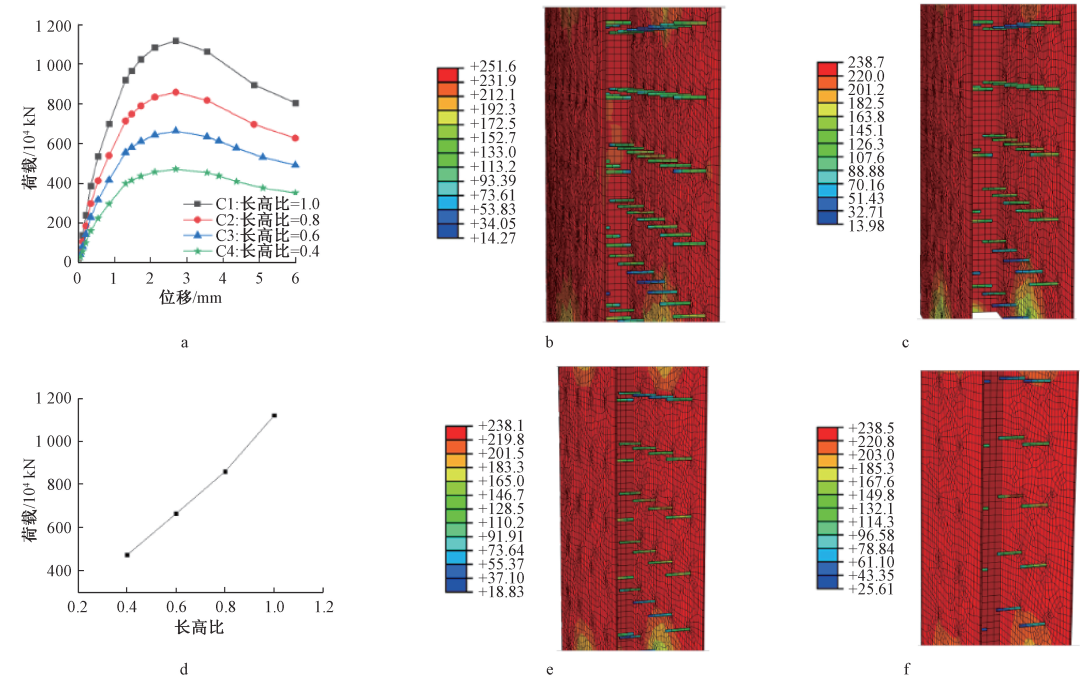
a——长高比对荷载-位移曲线的影响； b——C1试件极限载荷下的挠度轮廓，MPa； c——C2试件极限载荷下的挠度轮廓，MPa； d——长高比对极限承载力的影响，MPa； e——C3试件极限载荷下的挠度轮廓； f——C4试件极限载荷下的挠度轮廓，MPa。

图9 不同长宽比有限元试件数值模拟

3.2 混凝土硬度

通过改变混凝土硬度，观察混凝土硬度对组合弯矩墙的极限承载力和纵梁应力。 从图10a和图10b可以看出，随着混凝土硬度的增加，初始挠度保持不变，但有限元模型的承载力明显提高，但混凝土硬度和极限承载力呈线性下降。 从4个试件极限承载力阶段的挠度云图（图10b、c、e、f）可以看出，在相同条件下，随着混凝土硬度的增加，纵梁内侧所承受的挠度明显减小。 当混凝土硬度等于60 MPa时，翼缘内挠度接近试件的最大挠度，如图10f所示。 说明高强混凝土与拱圈的协同作用较强。

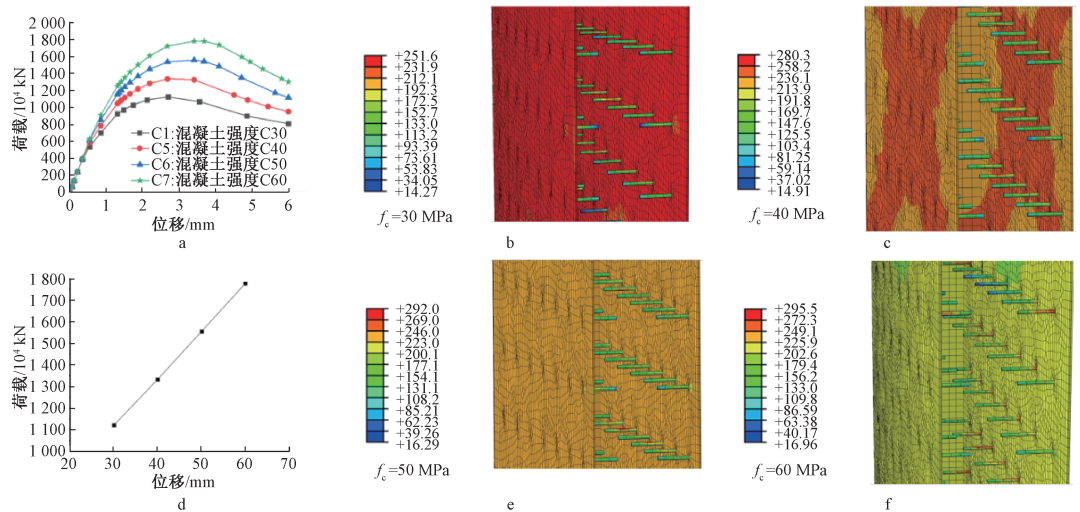
a——混凝土硬度对荷载-位移曲线的影响； b——C1试件极限载荷下的挠度云图，MPa； c——C5试件极限载荷下的挠度轮廓，MPa； d——混凝土硬度对极限承载力的影响； e——C6试件极限载荷下的挠度轮廓，MPa； f——C7试件极限载荷下的挠度轮廓，MPa。

图10 不同硬度混凝土有限元试件数值模拟

3.3 厚板硬度

随着厚板硬度的增加，有限元模型中的极限承载力有一定程度的增加，但厚板的硬度随试件的极限承载力呈线性下降，如图11a、d所示。 从相关文献可以看出，在极限承载力状态下，纵梁的最大挠度集中在试件中部的几个拱环处。 从各试件中部局部挠度云图（图11）可以看出，在C7试件中（厚板硬度与拱圈硬度相等时），中厚板和纵梁内侧可同时达到最大挠度范围321.7~348.6MPa。 表明当钢材硬度与纵梁相同时，拱圈的抗剪性能充分发挥，厚板与混凝土的协同作用更强，拱圈传递的弯矩会更大。

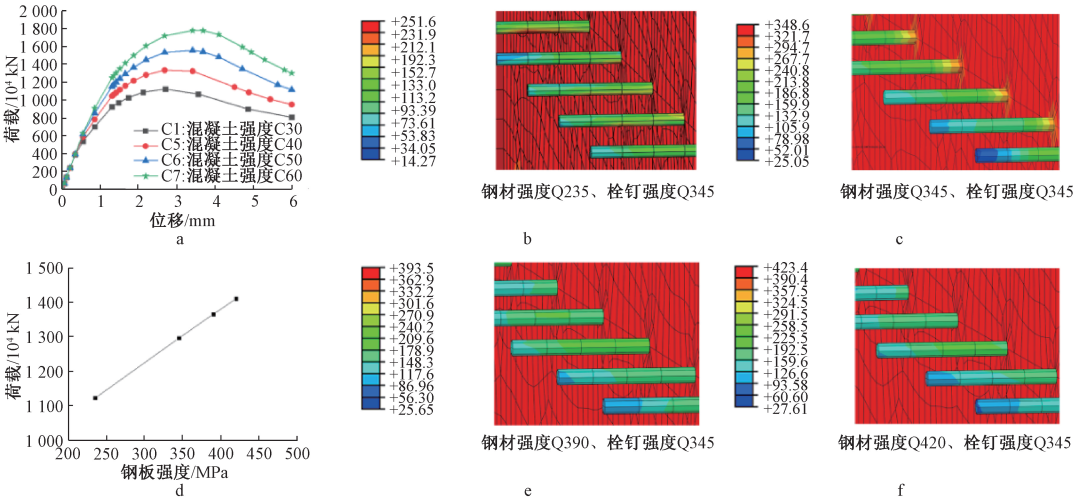
a——钢板硬度对载荷-位移曲线的影响； b——C1试件极限载荷下的挠度云图，MPa； c——C7试件极限载荷下的挠度轮廓，MPa； d——钢板硬度对极限承载力的影响； e——C8试件极限载荷下的挠度云图，MPa；

图11 厚板不同硬度有限元试件数值模拟

3.4 拱环硬度

作为柔性剪力连接件，拱圈硬度对试件极限承载力几乎没有影响，曲线基本重合，如图12a、d所示。 并且从图12c的挠度云图中可以看出，当钢材硬度与纵梁硬度相同时，拱圈内挠度可以达到最大值，拱圈的抗剪性能可以得到充分发挥，验证了3.3节中的推论。

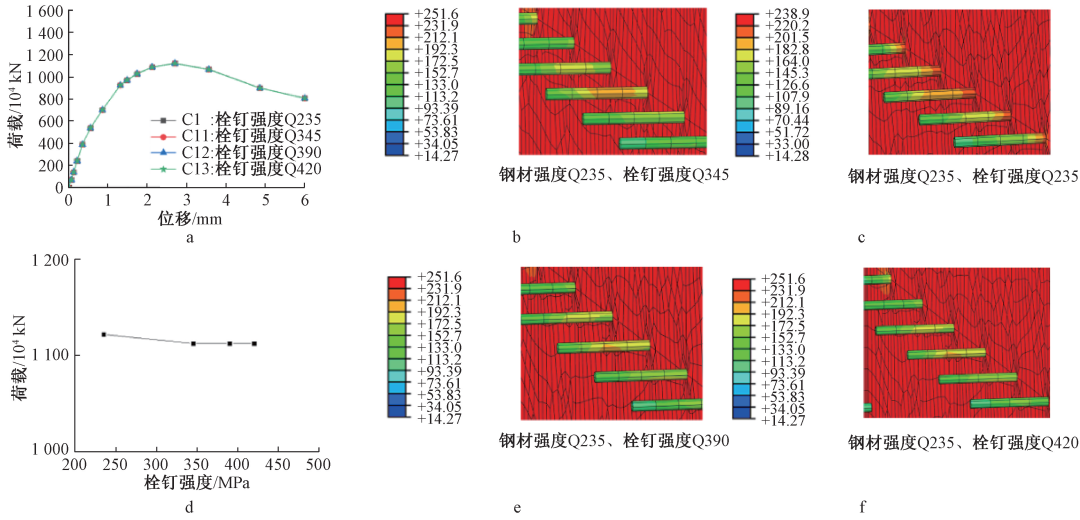
a——螺柱硬度对载荷-位移曲线的影响； b——C1试件极限载荷下的挠度云图，MPa； c——C11试件极限载荷下的挠度轮廓，MPa； d——螺柱硬度对极限承载力的影响； e——C12试件极限载荷下的挠度轮廓，MPa； f——C13试件极限载荷下的挠度轮廓，MPa。

图12 不同拱圈硬度的有限元试件数值模拟

4。结论

为了研究不同参数下厚板组合弯矩墙的极限承载力及纵梁受剪机理，本文模拟了试件中厚板的屈曲变形，并对参数进行了分析，得出以下推论：

1）本文选取的本构关系、接触关系和边界条件等有限元参数能够较好地模拟厚板混凝土组合弯矩墙的位移加载和破坏过程，荷载-位移曲线和厚板屈曲规律与试验现象一致。

2）长高比L/H、混凝土硬度、钢材硬度对试件极限承载力影响较大，且影响基本呈线性关系。 较小的长高比可以改善预制构件的脆性，拱圈的硬度对试件的极限承载力影响不大。

3）长高比越小，高强混凝土与拱圈的协同作用越强。

4）拱圈的挠度集中在内侧，当板的硬度与纵梁的硬度一致时，拱圈的内侧挠度可以达到较大的值，拱圈的抗剪性能可以充分发挥，与混凝土的协同作用更强。

资料来源：李静，卢无才。 厚板混凝土组合弯矩墙轴压模拟及拱环剪力数值参数研究[J].钢结构(中英文),2021,36(9):10-18.

DOI: 10.13206/j.gjgS20062202