热处理计算机模拟技术的发展前景分析-苏州安嘉

热处理作为材料加工的后续工序，对零件的性能和质量起着重要作用。 大型铸锻件由于尺寸大、重量重、截面积大，对性能要求较高。 因此，在热处理过程中，必须保证锻件内部温度均匀，充分完成奥氏体化过程，细化晶粒，消除内应力。 冷却过程中必须保证一定的冷却速率，以获得合适的组织，保证材料的性能。 同时，必须尽可能减少应力，以避免开裂的风险。 在热处理模拟中，存在温度场、组织场、应力场等多种场耦合。 组织场和应力场的计算取决于温度场，而温度场的计算取决于表面传热系数[1,2]。 因此，工件表面传热系数的准确计算对热处理数值模拟结果的准确性具有重要影响。

在以往的计算中，传热系数常以常数或经验公式的形式代入，但计算结果与实际略有不同。 由于传热系数受外部介质的性质和状态以及工件本身的热物理性质、形状、尺寸和表面状况等因素的影响，因此很难直接测量传热系数。 必须采用合理的计算方法并结合现场实际测量结果。 [3]。 随着数值计算理论和计算机技术的发展，热处理计算机模拟技术也得到了更多更好的应用。 学者们从实验和数值模拟两个方面对冷却过程的传热机理进行了深入研究。 莫拉莱斯[4]等人。 计算了不锈钢和合金钢在不同冷却介质下的表面综合传热系数； Jayanti[5] 等人。 采用流体力学方法计算了不同流量下的表面传热系数； L Syhakhang[6] 等人。 通过零件不同位置的冷却曲线计算传热系数，并应用有限元方法模拟零件的温度场。 结果表明，计算曲线与实测曲线吻合较好； 黄鹏[7]等。 使用一维和三维有限元。 采用逆传热法对数学模型进行求解，利用得到的传热系数计算出工件心部温度随时间的变化曲线，与实测结果吻合较好； 谷建峰[8]等采用逆传热法计算了工件在动态淬火介质中的变化曲线。 测量了介质冷却过程的传热系数。 本文采用逆传热法中的非线性估计方法对9Cr钢阶梯试件正火过程中的传热系数进行了估算，并利用DEFORM软件对阶梯试件的整个正火过程进行了模拟，得出以下结论： 9Cr钢吹冷温度场和组织场的分布。

1 研究方法

1.1 理论基础

热交换过程和温度场变化是热处理过程中最值得关注的问题。 根据能量守恒原理，由弗卢里叶热传导方程可以推导出固态热传导的控制方程。

式中：λ——材料的导热系数（W/m·℃）； q′——内部热源热流密度（W/m2）； T——温度（℃）； t——处理时间（s）； ρ——材料密度（kg/m3）； cP——材料的定压比热(J/(kg·℃))。

稳态条件下，最基本的傅里叶定律可以描述为：热流量与温差成正比，热流量与垂直于热流方向的表面积成正比。 对于一个具体问题，为了获得方程的唯一解，必须给出初始条件和边界条件。

初始条件是指初始温度场。 可以是均匀的，如将锻件从室温加热到炉中，或者加热到给定温度并长时间保温，使工件的内部和外部都被充分加热。

，式中T0（℃）为已知温度； 初始温度场也可能不均匀，此时

是已知的温度函数。本文的研究首先从恒温加热到奥氏体化温度，然后正火。 假设初始条件是均匀的，即

。

边界条件是指工件外表面与周围环境之间的热交换。 在传热中，边界条件概括为三类：

第一类边界条件：物体边界上的温度或温度函数已知，用公式表示为

在公式：

——物体的边界范围； Tw——已知工件表面温度（℃）； f(x,y,z,)t——已知工件表面温度函数，随时间和位置变化。

第二类边界条件是指物体表面的热流密度qw已知，规定热流密度q的方向与边界外法线n的方向相同，且其表达式为：

式中：qw——已知工件表面热流密度，为固定值（W/m）2； g(x,y,z,t)——已知工件表面热流密度函数，它随位置和时间而变化。

第三类边界条件也称为牛顿对流边界，是指物体与与其接触的流体介质之间的对流换热系数Hk和介质温度Tf已知，其表达式为：

本文涉及的边界条件为第三类边界条件，即传热系数输入法。 表面传热系数（简称传热系数）表示单位时间、单位面积内工件表面与流体介质的平均温差为1℃时，工件表面与流体介质之间传递的热量。 在热处理过程的数值模拟中，组织场和应力场的计算依赖于温度场，而传热系数是计算温度场的重要参数之一。 因此，传热系数的准确测量和合理选择对于热处理过程尤其是冷却过程的数值模拟具有重要意义。最常用的是对流与辐射混合的传热边界[9]，其表达式为

式中：H——总传热系数，H=Hk+Hs； Hs——辐射传热系数，

式(5)中的温度值采用绝对温度； σ为Stefan-Boltzmann常数，其值为5.768×10-8W/(m2·K4)； ε表示工件表面发射率。

设备或工件表面与大气之间的自然对流换热可采用以下经验公式：

反演传热法利用反演法中的非线性估计方法来计算传热系数。 在具体计算中，首先根据上述理论基础中给出的经验公式（见式（5）和（6））设定初始传热系数，然后利用有限元方法计算出该温度下的温度曲线测量点。 根据计算出的温度曲线与实际测量温度曲线的比较结果，不断修正给定的初始传热系数值，然后用修正后的传热系数值重新计算测温点的温度曲线。 重复此过程，直到计算出的曲线无限接近实际测量的曲线。 即可求出该条件下的传热系数值。

1.2 测温测试

本文所述的测试采用无纸记录仪跟踪梯形试件在整个正火过程中的温度随时间的变化曲线。 在梯形试件几何模型厚度的1/2处（见图1（a））布置4个测温点（见图1（b））。 梯形试件处的热电偶连接至外部无纸记录仪。 由于梯形试件最厚壁厚达到500毫米，整个正火过程耗时较长，因此无纸记录仪每1分钟采集一次数据。 试验开始后，将梯形试件装入台车式热处理炉内加热保温。 保温完毕后，打开炉门，将梯形试件运至吹冷现场进行正火冷却。 整个转移过程持续约20分钟。

如果采集到的温度曲线比较振荡，为了避免和最小化实际测量中产生的波动误差，首先对温度曲线数据进行拟合，得到平滑的曲线。 本实验中，由于实际测量的温度曲线比较平滑，因此没有进行二次拟合处理。

1.3 数值模型

对梯形试件进行几何建模并划分网格。 考虑到计算精度和效率，采用六面体网格划分（见图2），网格数为18750个，节点数为21788个。 利用DEFORM软件对梯形试件进行数值模拟。 给出如下边界条件：梯形试件初始时刻内部无温差，初始组织主要为马氏体，有少量残余奥氏体。 内部残余应力为零，表面各部位传热条件一致。

2 结果与分析 2.1 表面传热系数计算结果与分析

根据热电偶在靠近表面的一点（P1点距表面20mm）处测得的实际温度曲线，采用逆传热法计算传热系数。 将P1点加热保温过程的实际测量温度曲线与模拟计算温度曲线进行比较（见图3（a））。 其中，实线为实测温度曲线，虚线为数值模拟温度曲线。 实际测量值与模拟值基本一致。 但在加热过程中，模拟值略高于测量值。 这是由于实际正火热处理过程中升温较快时，存在热处理炉内温度均匀的问题，而数值模拟过程中假设是均匀的，因此升温过程中的模拟值稍大比实际测量值。 随着时间的推移，热处理炉各处的温差逐渐缩小直至基本均匀，因此后续过程中模拟曲线与实测曲线基本吻合。 比较冷却过程的实测曲线和模拟曲线（见图3（b）），两者基本重合，但在400-150℃阶段存在差异。 这是由于相变潜热的作用。 虽然模拟中考虑了相变潜热，但相变潜热数据来自理论计算并被设置为恒定值，而实际上相变潜热是温度的函数。

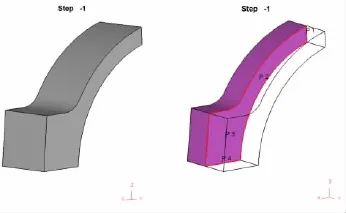
图1 梯形试件几何模型及耦合位置示意图

(a) 阶梯试件的几何模型 (b) 阶梯试件的耦合位置

图2 梯形试件六面体网格划分

应用获得的传热系数（见图4）来模拟其余三点的温度曲线。 左边(a)实线是加热保温过程中的传热系数，右边(b)实线是空气冷却过程中的传热系数。 虚线为吹风冷却过程中的传热系数。 将现场测温结果与模拟结果进行对比（见图5），可以发现温度曲线基本重合，吻合较好。 冷却过程中P3点温度曲线的测量结果显示有小凸起。 这是因为P3点位于厚壁的中心，积聚了大量的相变潜热。 因此，在模拟计算中，厚壁处的温度曲线平滑下降，而实测温度较高时会出现小凸点。

2.2 数值模拟结果及分析

阶梯试件初始时刻的温度为50℃，初始组织含有约85%的马氏体和15%的奥氏体。 加热完成后，阶梯试件表面温度高于1080℃，内部温度1 050℃(见图6)，表面和心部均奥氏体化(见图7)。 约1.5小时后，表面开始达到设定温度。 4.5小时后，整个外表面达到设定温度。 又过了5小时10分钟，核心达到设定温度。

图3 P1点实测曲线与模拟曲线

图4 正火过程传热系数

图5 正火过程中不同位置的温度曲线

保温结束时，梯形试件内外温度分布均匀，全部为奥氏体组织。 然后，转移（空气冷却20分钟）。 在吹冷过程开始之前，梯形试件的表面温度已降至约900℃。 ℃左右，心脏最高温度为1096℃（见图8）。

图6 梯形试件加热结束时的温度分布

图7 梯形试件加热结束时的组织野分布

开始吹风降温5分钟后，表面温度降至850℃左右，核心温度下降17℃（见图9（a））； 15分钟后，表面温度降至750℃左右，核心温度下降49℃（见图9（a）、图9（b））； 30分钟后，表面温度降至650℃左右，核心温度下降106℃（见图9（c））； 吹冷1小时后，表面温度降至500℃左右，核心温度降至500℃左右。 下降了 178°C（见图 9（d））。 此时，一小部分表面的温度已开始低于Ms点温度，表面开始出现微量的马氏体组织（见图10（a））； 吹风冷却3小时后，表面温度降至250℃左右，核心温度下降382℃（见图9（e））。 薄壁表面和薄壁心部的马氏体转变量达到70%以上，组织转变基本完成，而厚壁部分仅在边缘处有马氏体组织，但马氏体地表中心和厚壁中心尚未出现结构(图10(b)); 鼓风冷却5小时后，表面温度降至100℃左右，中心温度也下降。 174°C（见图 9(f)）。 此时表面和心部的马氏体转变量均在85%以上（见图10（c））。 继续冷却到室温左右，98%以上的组织转化就完成了。

图8 梯形试件空冷20分钟后的温度分布

3 结论

(1)利用无纸记录仪测量梯形试件在实际正火过程中的温度变化曲线，利用逆传热法中的非线性估计方法计算加热和保温过程中的传热，空气冷却和空气冷却工艺。 系数。

(2)利用得到的传热系数模拟梯形试件多个位置的温度变化曲线，与实际测量结果吻合较好，进一步验证了给定传热系数的合理性和有效性。

(3)利用DEFORM软件对梯形试件的正火过程进行数值模拟，得到不同时间的温度场和组织场。 结果表明，炉温达到温度后，整个试件达到设定温度大约需要5 h 10 min。 冷却过程中，开始时表面温度下降很快，核心温度下降缓慢。 随着冷却过程的继续，表面温度下降缓慢且缓慢，而核心温度下降速度较快。 空冷1小时后，表面开始出现微量马氏体； 经过3小时的空冷，薄壁的结构转变基本完成，厚壁表面的中心开始发生结构转变。 空冷5小时后，整个试片85%以上组织转变完成，继续冷却至室温，组织转变完成。

图9 阶梯试件吹风冷却后的温度分布

(f) 鼓风冷却5 h后的温度分布

图10 空冷阶梯型试件的显微组织分布

引用: 王才山，张雪娇，杨康，等。 9Cr钢正火过程传热系数计算及数值模拟[J]. 第一重科技，2018，（2）：30-36。