小升初毕业“总复习”—六年级数学 专题讲解及训练（2）含答案

已保存

小学数学总复习讲解与训练（二）

练习测试题

1、气缸容积

1. 求下面每个圆柱体的体积。

(1)底座面积0.6平方米，高度0.5米

(2) 底部半径为3厘米，高度为5厘米。

(3)底部直径8米，高10米。

(4)底座周长25.12分米，高2分米。

2. 有两个底面积相等的圆柱体。 第一个圆柱体的高度是第二个圆柱体的4/7。 第一个圆柱体的体积是24立方厘米。 第二个圆柱体的体积比第一个圆柱体大多少立方厘米？

3、在直径0.8米的水管中，水流速度为每秒2米。 1分钟流过多少立方米水？

4、牙膏出口直径为5毫米。 小红每次刷牙都会挤出1厘米的牙膏。 这款牙膏可以使用36次。 该品牌牙膏推出的新包装仅将出料口直径改为6毫米。 小红还是像往常一样挤出了1厘米长的牙膏。 那么，这款牙膏可以使用多少次呢？

5、将圆柱形钢材截断1.5米，测量其横截面直径为4厘米。 如果钢材每立方厘米重 7.8 克，那么切割下来的钢材重多少公斤？ （保留数字以千克为单位。）

6. 将边长为 6 分米的木块切成最大的圆柱体。 这个圆柱体的体积是多少立方分米？

7、右图是一个圆柱体。 如果它的高度缩短3厘米，它的表面积就会减少94.2平方厘米。 这个圆柱体的体积减少了多少立方厘米？

2. 锥体体积

1.多项选择题。

(1) 圆锥体的体积为立方米，同底同高的圆柱体体积为 ( )

①

一立方米 ② 3a立方米 ③ 9立方米 （2）将一段圆钢切成最大的圆锥体。 圆柱体的体积为6立方米，圆锥体的体积为( )立方米。

① 6立方米 ② 3立方米 ③ 2立方米

2、判断对错。

(1)圆柱体的体积相当于圆锥体体积的3倍……()

(2)将一根木头圆柱体加工成最大的圆锥体。 去掉部分的体积与圆锥体的体积之比为2:1...()

(3) 圆柱体和圆锥体同底同高。 体积相差21立方厘米。 圆锥体的体积为7立方厘米。

…………（）

3.填空

(1) 圆柱体的体积为 18 立方厘米，同底同高的圆锥体的体积为 ( ) 立方厘米。

(2)圆锥体的体积是18立方厘米，与其底同高的圆柱体的体积是()立方厘米。

(3)同底同高的圆柱体和圆锥体的体积之和是144立方厘米。 圆柱体的体积为 ( ) 立方厘米，圆锥体的体积为 ( ) 立方厘米。

4. 求下列圆锥体的体积。

(1) 底部半径为 4 厘米，高度为 6 厘米。

(2)底部直径6分米，高8厘米。

(3)底周长31.4厘米，高12厘米。

5、圆锥形沙堆高1.5米，底部半径2米。 每立方米沙重1.8吨。 这堆沙子重多少吨？

6、近圆锥形的麦堆，底周长12.56米，高1.2米。 如果每立方米小麦重750公斤，那么这堆小麦重多少公斤？

7、一个长方形的容器，长5厘米，宽4厘米，高3厘米。 加满水后，将水全部倒入高度为6厘米的锥形容器中，直至完全充满。 这个圆锥形容器的底面积是多少平方厘米？

参考答案：

1、气缸容积

1. 求下面每个圆柱体的体积。

（1）底面积0.6平方米，高度0.5米0.6×0.5=0.3（立方米）

(2) 底部半径为3厘米，高度为5厘米。 3.14×3²×5=141.3（立方厘米）

(3)底部直径8米，高10米。 3.14×(8÷2)²×10 = 502.4（立方米）

(4)底座周长25.12分米，高2分米。

3.14 × (25.12÷3.14÷2)² × 2 = 100.48（立方分米）

2. 有两个底面积相等的圆柱体。 第一个圆柱体的高度是第二个圆柱体的4/7。 第一个圆柱体的体积是24立方厘米。 第二个圆柱体的体积比第一个圆柱体大多少立方厘米？

对于底面积相同的两个圆柱体，第一个圆柱体的高度是第二个圆柱体的4/7，第一个圆柱体的体积也是第二个圆柱体的4/7。

24 ÷ 4/7 – 24 = 18（立方厘米）

答：第二个圆柱体的体积比第一个圆柱体大 18 立方厘米。

3、在直径0.8米的水管中，水流速度为每秒2米。 1分钟流过多少立方米水？

3.14×(0.8÷2)²×2×60=60.288（立方米）

答：那么1分钟内流过60.288立方米的水。

4、牙膏出口直径为5毫米。 小红每次刷牙都会挤出1厘米的牙膏。 这款牙膏可以使用36次。 该品牌牙膏推出的新包装仅将出料口直径改为6毫米。 小红还是像往常一样挤出了1厘米长的牙膏。 那么，这款牙膏可以使用多少次呢？

牙膏体积：1厘米=10毫米

3.14 × (5÷2)² × 10 × 36 = 7065（立方毫米）

7065 ÷ [3.14 × (6÷2)² × 10] = 25（次）

答：这样一来，这款牙膏只能使用25次。

5、将圆柱形钢材截断1.5米，测量其横截面直径为4厘米。 如果钢材每立方厘米重 7.8 克，那么切割下来的钢材重多少公斤？ （保留数字以千克为单位。）

1.5米=150厘米

3.14×(4÷2)²×150×7.8=14695.2(克)=14.6952(千克)≈15(千克)

答：切下的这块钢材重 15 公斤。

6. 将边长为 6 分米的木块切成最大的圆柱体。 这个圆柱体的体积是多少立方分米？

3.14 × (6÷2)² × 6 = 169.56（立方分米）

答：这个圆柱体的体积是169.56立方分米。

7、右图是一个圆柱体。 如果它的高度缩短3厘米，它的表面积就会减少94.2平方厘米。 这个圆柱体的体积减少了多少立方厘米？

底围：94.2÷3 = 31.4 厘米

3.14 × (31.4÷3.14÷2)² × 3 = 235.5（立方厘米）

答：这个圆柱体的体积减少了235.5立方厘米。

2. 锥体体积

1.多项选择题。

(1) 圆锥体的体积为立方米，同底同高的圆柱体的体积为 (②)

①

一立方米 ② 3a立方米 ③ 9立方米 （2）将一段圆钢切成最大的圆锥体。 圆柱体的体积为6立方米，圆锥体的体积为(③)立方米

① 6立方米 ② 3立方米 ③ 2立方米

2、判断对错。

(1)圆柱体的体积相当于圆锥体体积的3倍...(×)

(2)将一块圆柱形木料加工成最大的圆锥体。 去掉部分的体积与圆锥体积之比为2:1……(√)

(3) 圆柱体和圆锥体同底同高。 体积相差21立方厘米。 圆锥体的体积为7立方厘米。

…………（×）

3.填空

(1)圆柱体的体积为18立方厘米，同底同高的圆锥体的体积为(6)立方厘米。

(2)圆锥体的体积为18立方厘米，同底同高的圆柱体的体积为(54)立方厘米。

(3)同底同高的圆柱体和圆锥体的体积之和是144立方厘米。 圆柱体的体积为（108）立方厘米，圆锥体的体积为（36）立方厘米。

4. 求下列圆锥体的体积。

(1) 底部半径为 4 厘米，高度为 6 厘米。

×3.14 ×4 ²×6 = 100.48（立方厘米） （2）底部直径为6分米，高度为8厘米。

×3.14×(60÷2)²×8 = 7536（立方厘米） (3) 底周长为31.4厘米，高为12厘米。

×3.14×(31.4÷3.14÷2)²×12 = 314（立方厘米） 5、圆锥形沙堆高1.5米，底部半径2米，每立方米沙重1.8吨。 这堆沙子重多少吨？

×3.14 ×2 ²×1.5×1.8 = 11.304（吨） 答案：这堆沙子重约11.304吨。

6、近圆锥形的麦堆，底周长12.56米，高1.2米。 如果每立方米小麦重750公斤，那么这堆小麦重多少公斤？

×3.14× (12.56÷3.14÷2)²×1.2 ×750 = 3768（公斤） 答案：这堆小麦重 3768 公斤。

7、一个长方形的容器，长5厘米，宽4厘米，高3厘米。 加满水后，将水全部倒入高度为6厘米的锥形容器中，直至完全充满。 这个圆锥形容器的底面积是多少平方厘米？

5 × 4 × 3 = 60（立方厘米）

60 × 3 ÷ 6 = 30（平方厘米）

答：这个圆锥形容器的底面积是30平方厘米

小学数学总复习讲解与训练（6）

主要内容

比例的含义和基本性质

学习目标

1.使学生初步了解图形的放大和缩小，能够利用方格纸将简单图形按一定比例放大或缩小，初步体验图形的相似性，进一步发展空间概念。

2.使学生结合图形的放大、缩小了解比例的意义和作用，理解比例的“术语”、“内部术语”、“外部术语”； 理解和掌握比例的基本性质，并能运用比例的基本性质解决比例问题。

3.学生在理解和应用比例的过程中，可以进一步理解不同领域数学内容的内在联系，增强运用数字和图形描述现实生活问题的意义和能力，丰富解题策略，培养数学能力。对数学的积极情绪。

测试点分析

1、按一定比例放大或缩小图形，就是将图形的各边按一定比例放大或缩小。

2. 表示两个比率相等的表达式称为比例。

3. 组成比例的四个数字称为比例项。 两端的两项称为比率的外项，中间的两项称为比率的内项。

4. 在比率中，两个外部项的乘积等于两个内部项的乘积。 这称为比例的基本性质。

5. 根据比例的基本性质，如果已知比例中的任意三项，则可以求出比例中的另一个未知项。 求比例的未知项称为求解比例。

典型例子

例1.（将图形按一定比例放大或缩小，形状不变，但大小改变。）

AB

(1) 矩形A的长为1.5厘米，宽为1厘米； 长方形B的长是3厘米，宽是2厘米。 这两个长方形的长度有什么关系？ 宽度怎么样？

(2) 如果将矩形 A 按 1:2 的比例缩小，则其长和宽应分别占原来的几分之几？ 各有多少个？

分析与解答： (1) 矩形B的长度是矩形A的两倍，宽度也是矩形A的两倍，换句话说，矩形B与矩形A的长度比为2:1，宽度的比例也是2:1。

将矩形的每条边放大到原始大小的两倍。 放大后的矩形与原矩形的长宽比为2:1。 这意味着矩形A的长度和宽度以2:1的比例放大。

(2) 将矩形A按照1:2的比例缩小到矩形C，并将长和宽缩小到原来的值。

，图片C的长度为0.75厘米，图片C的宽度为0.5厘米。 可以看出，放大或缩小前后图形的形状没有变化。 它仍然是矩形，但大小发生了变化。

例2.（根据指定比例，图形将根据需要放大或缩小）

先按3:2的比例画出矩形A的放大图B，再按1:2的比例画出矩形A的缩小图C。 (1) 图 B 的长和宽是多少？ （2）图C呢？ （3）观察这三个图形，你发现了什么？

分析与解决：（1）将矩形A按3：2的比例放大，即矩形A的长和宽分别扩大1.5倍。 那么图片B的长度为6×1.5=9个方格，宽度为4×1.5=6个格子。 （2）按照1:2的比例缩小矩形A，即将矩形A的长和宽分别缩小到原来的值。

，则图C的长度为6÷2=3格，宽度为4÷2=2格。 (3) 从这三个不同尺寸的图形可以看出，放大或缩小后的图形与原图相比，虽然尺寸发生了变化，但形状保持不变，且各边长度的变化与原图一致。指定比例。 。 点评：按比例放大或缩小图形的关键是首先根据比例确定是否放大或缩小，然后确定各边的长度，然后绘制图形。

例3.（将两个相等的比率写入一个方程）

图B是图A的放大图，你能写出两张图的长宽比吗？ 比较所写的两个比率，你发现了什么？

3厘米

6厘米

4厘米

8厘米

分析与解决：（1）图A中长宽比为4：3； 图B中原来的长宽比是8:6，8:6简化为4:3。

(2) 简化后，这两个比率都是4:3，并且比率相等，说明这两个比率可以写成一个方程。此时

4:3 = 8:6 或

，两者读作：4比3等于8比6。 例4.（理解比例）下列组中哪两个比可以构成一个比例？ 写出比例。

(1) 5:6 和 15:18 (2) 0.2:0.1 和 3:1

(3)

：

和 1.2: 0.8 (4) 6: 2 和

：

分析与解答：求每组中两个比值的比值。 如果相等，则可以形成比例。 如果它们不相等，就不能形成比例。

(1) 因为 5:6 =

,15:18=

，所以 5:6 = 15:18。 (2) 因为0.2:0.1 = 2 和3:1 = 3，所以0.2:0.1 和3:1 不能形成比率。

（3）因为

：

, 1.2:0.8 =

，所以

：

= 1.2:0.8。 (4)6：2=3，

：

= 3，所以 6:2 =

：

。 评语：判断两个比率能否构成比例，可以按照题中的方法求出两个比率的比值。 如果比例相等，则可以形成比例，否则不起作用。 解决这个问题的基础是比例的意义。

例5.（比例各部分的名称及比例的基本性质）

一台织布机3小时可织3.6米的布，4小时可织4.8米的布。 你能根据数量之间的关系写出一个比率吗？

分析与解决：（1）这台织机织出的织物米数与织造时间之比相等。 3.6:3 = 4.8:4

(2)该织机织造的织物米数之比等于织造时间之比。 3.6:4.8 = 3:4

(3)该织机的织造时间与织造米数之比相等。 3:3.6 = 4:4.8

介绍“项”：组成比例的四个数字称为比例项。 两端的两项称为比率的外项，中间的两项称为比率的内项。 例如：

3.6:3 = 4.8:4

内部术语

外部物品

关于观察问题中的三个比率，你发现了什么？

3.6: 3 = 4.8: 4 3.6: 4.8 = 3: 4 3: 3.6 = 4: 4.8

(1) 3.6和4可以同时用作比率的外项，也可以同时用作比率的内项。

(2) 3.6 × 4 = 3 × 4.8。 可以看出，比率中两个外部项的乘积等于两个内部项的乘积。

(3) 如果将3.6:3 = 4.8:4改写为分数

，等号两边的分子和分母分别叉乘，结果也相等。 (4) 如果用字母来表示比率的四项，即a : b = c : d，

那么这条规则可以表示为ad=bc或bc=ad。

(5) 按比例，两个外部项的乘积等于两个内部项的乘积。 这称为比例的基本性质。

例 6. （比例基本性质的应用）根据方程 2 × 7 = 1.4 × 10 写出几个比例。

分析与解答：根据比例的基本性质，可以得出两组数字2和7、1.4和10要么同时为比例的外项，要么同时为比例的内项时间。

1.4 : 2 = 7 : 10 1.4 : 7 = 2 : 10

10:2=7:1.4 10:7=2:1.4

2：1.4 = 10：7 2：10 = 1.4：7

7: 1.4 = 10: 2 7: 10 = 1.4: 2

评语：这样一共可以写出8个比例。 但他们没有改变的是，2和7要么同时是内部项，要么同时是外部项，对于数字1.4和10的集合也是如此。书写时可以分组书写。

例7.（放大的意义）

王叔叔在电脑上放大了下面的图片。 放大图的长度是12.5厘米。 你发现了什么？

4厘米

5厘米

分析与解决：按比例放大是指将原图形中的所有线段按相同比例放大。 相关线段放大前后的厘米数可以成比例。 两张图片的长和宽之比可以形成比例，两张图片的长和宽之比也可以形成比例。

12.5 : 5 = 宽度: 4 或 12.5 : 宽度 = 5 : 4

例8.（比例尺的解法）上图中的宽度是多少厘米？

分析与求解：求解比例时，根据比例的基本性质将比例转化为乘积等式方程，然后根据方程的性质求解。

解：设宽度为ⅹ厘米。

12.5 : 5 = ⅹ : 4

5ⅹ = 12.5 × 4 ┈┈ 根据比例的基本性质

5ⅹ = 50

ⅹ = 10

答：图片放大后的宽度为10厘米。

注释：像上面这样找到比率中的未知项称为求解比率。

同学们，你会回答

是这个比例吗？ 试一试！ 小学数学总复习讲解与训练（6）

练习测试题

1、长方形图片一张，长12厘米，宽9厘米。 按1:3的比例缩小后，新图片的长度为（ ）厘米，宽度为（ ）厘米。 该图片（ ）保持不变，其大小为（ ）。

2、边长10厘米的方形花手帕。 按( )的比例放大后，边长变为30厘米。

3、以2:1的比例画一个放大的平行四边形，以1:3的比例画一个缩小的矩形。

4. 应用比例的含义，判断下列两个比例中哪一个可以构成比例？

6:10 和 9:15 20:5 和 4:1 5:1 和 6:2

5、2：5、12：0.2、310：15这三个比例中，能与5.6：14组成比例的是（）。

6. 按比例计算，两个 ( ) 的乘积等于两个 ( ) 的乘积。

7、若A×3=B×5，则A:B=():()。

8. 从 6、24、20、18 和 5 五个数字中选择四个数字，组成一个比率：

( ) ∶ ( ) = ( ) ∶ ( )。

9. 根据3×8 = 4×6 写出的比率是( )、( ) 或( )。

10. A 数的 25% 等于 B 数的 75%，则 A 数与 B 数之比为 ( ): ( )。

13. 求解比例

ⅹ∶3 = EQ \F(7,8) ∶ EQ \F(1,4) EQ \F(9,x) = EQ \F(4.5,0.8) EQ \F(1,6) ∶ EQ \F (2,5) = EQ \F(1,2) ∶x

EQ \F(3,4) ∶ x = 3∶12 EQ \F(3,8) ∶ x = 5%∶0.6 EQ \F(1.3,18) = EQ \F(x,3.6)

14. 在一个比率中，两个外项的乘积是 30。已知一个内项是 10，另一个内项是 ( )。

参考答案：

1、长方形图片一张，长12厘米，宽9厘米。 按照1:3的比例缩小后，新图片的长度为（4）厘米，宽度为（3）厘米。 这张图的（形状）不变，但是大小（变化）。

2、边长10厘米的方形花手帕。 按照（3：1）的比例放大后，边长变为30厘米。

3、以2:1的比例画一个放大的平行四边形，以1:3的比例画一个缩小的矩形。

4. 应用比例的含义，判断下列两个比例中哪一个可以构成比例？

6:10 和 9:15 20:5 和 4:1 5:1 和 6:2

(1) 因为 6:10 =

,9:15=

，所以 6:10 = 9:15。 (2) 因为 20:5 = 4 且 4:1 = 4，所以 20:5 = 4:1。

(3) 因为5:1 = 5 和6:2 = 3，所以5:1 和6:2 不能形成比率。

5、2：5、12：0.2、31：15这三个比例中，能与5.6：14形成比例的是（2：5）。

6. 在比率中，两个（外部项）的乘积等于两个（内部项）的乘积。

7、若A×3=B×5，则A∶B=（5）：（3）。

8. 从 6、24、20、18 和 5 五个数字中选择四个数字，组成一个比率：

(6): (24) = (5): (20)。 6×20 = 24×5 可以组成8个比例

9、按照3×8=4×6写出的比例为（3:4=6:8）、（3:6=4:8）或（4:3=8:6）。可以组成8比例

10. A 数的 25% 等于 B 数的 75%，则 A 数与 B 数之比为（3）：（1）。

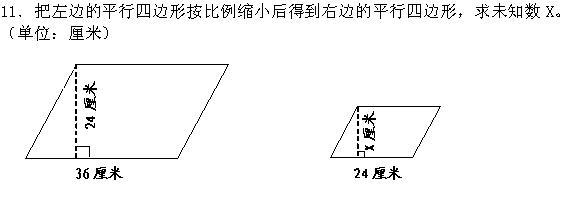
解：设平行四边形的高为ⅹ厘米。

36 : 24 = 24 : ⅹ

36ⅹ = 24 × 24 ┈┈ 根据比例的基本性质

36ⅹ = 576

ⅹ = 16

答：平行四边形的高是16厘米。

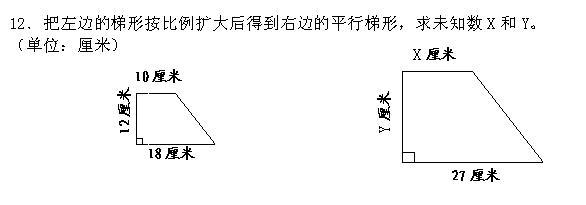
解：设梯形的上底为ⅹ厘米，高为Y厘米。

18 : 27 = 10 : ⅹ 18 : 27 = 12 : 是

18ⅹ = 27 × 10 18 Y = 27 × 12

18ⅹ = 270 18 Y = 324

ⅹ = 15 Y = 18

答：梯形的上底长是15厘米，高是18厘米。

13. 求解比例

ⅹ∶3 = EQ \F(7,8) ∶ EQ \F(1,4) EQ \F(9,x) = EQ \F(4.5,0.8) EQ \F(1,6) ∶ EQ \F (2,5) = EQ \F(1,2) ∶x

ⅹ=

ⅹ = 1.6 ⅹ = 1.2EQ \F(3,4) ∶ x = 3∶12 EQ \F(3,8) ∶ x = 5%∶0.6 EQ \F(1.3,18) = EQ \F(x, 3.6)

ⅹ = 3 ⅹ = 4.5 ⅹ = 0.26

14. 在一个比率中，两个外项的乘积是 30。已知一个内项是 10，另一个内项是 (3)。

小学数学总复习讲解与训练（7）

主要内容

缩放、面积变化、确定位置

学习目标

1.使学生在具体情况下理解比例的含义，理解线段比例。 可以求出图片的比例尺，可以根据给定的比例尺求出对应的实际距离或图片上的距离，并可以转换数值比例尺和线段比例尺。

2.让学生在“猜测与验证”的过程中，独立发现平面图形按比例放大时面积的变化规律。

3.在解决问题的过程中，进一步体会比例和尺度的应用价值，感知不同领域数学内容之间的内在联系，增强运用数字和图形描述现实问题的意识和能力，丰富问题- 解决策略。

4.使学生初步了解具体情况下北偏东（西）、南偏东（西）的含义，初步掌握利用方向和距离确定物体位置的方法，并能判断物体上的物体。基于给定方向和距离的平面图。 位置或描述简单的步行路线。

5.在利用方向和距离确定物体位置的过程中，学生可以进一步培养观察能力、图片识别能力和有组织的表达能力。 发展空间概念。

6.使学生积极参与观察、测量、绘画、交流等活动，获得成功经验，了解数学知识与现实生活的联系，拓展知识视野，激发学习兴趣。

测试点分析

1、图片上的距离与实际距离的比值称为图片的比例尺。

2. 规模=

，比例尺有两种形式：数字比例尺和线段比例尺。 3、将平面图形按一定倍数（n）放大或缩小到原尺寸的几分之一（

），放大（或缩小）后与放大（或缩小）前的图形面积比为n²：1（或1：n²）。 4、知道物体的方向和距离就可以确定物体的位置。

5、根据物体的位置，结合比例尺的相关知识，可以在平面图上画出物体的位置。 画图时，先根据方向画一条射线，然后根据图上的距离找到该点的位置。

6.逐条描述步行路线，每段应写明步行的方向和距离。

典型例子：

示例 1.（了解比例）

王叔叔家有一块长方形的菜地，长40米，宽30米。 将菜地缩小到一定比例，以长4厘米、宽3厘米的方式绘制在平面图上。 你能写出地图上的菜地长和宽的距离与实际距离的比值吗？

分析及解决：地图上的距离和实际距离单位不同。 必须先统一为同一单位，写出比率，然后化简。

40 米 = 4000 厘米 3 厘米 = 0.03 米

图片上的距离与实际距离的比值称为图片的比例尺。

地图上的距离：实际距离=比例尺或

= 比例尺地图上的距离与实际距离的比例为1:1000。 该地图的比例尺为1:1000，也可以写为

，仍然读作1到1000。 点评：求地图的比例尺是一个相对简单的问题。 这样做唯一需要注意的是末尾0的问题：第一，将米和公里换算成厘米时，必须在米和公里数的末尾添加2个或5个0； 第二，求秤的结果时，一定要注意0的个数。 如果你数一数、想一想，就不会出错。

例2.（音阶的理解以及音阶的两种表达方法）

比例尺 1:1000 表示地图上的距离是实际距离的几分之一？ 实际距离是图片上距离的多少倍？ 图片中的1厘米代表实际距离是多少米？

分析与解决：比例尺1：1000表示地图上的距离为实际距离。

，实际距离是图片上距离的1000倍。 图片上1厘米的距离代表实际距离1000厘米，也就是10米。 像1:1000这样的比例尺称为数值比例尺。1:1000的比例尺也可以这样表示

0 10 20 30 米

，这是一个线段比例尺，也就是说图上1厘米的距离代表实际距离10米。

示例 3. 手表零件绘制在图片上时长 2 毫米和 4 厘米。 这幅画的比例是多少？

错误解： 4 厘米 = 40 毫米 2 : 40 = 1 : 20

思路分析：无论什么样的图，比例始终是图上的距离与实际距离的比值。 根据比例尺的定义，用“图纸上的距离：实际距离=比例尺”来求。

正确答案：4 厘米 = 40 毫米 40 : 2 = 20 : 1

点评：标尺通常应该写成前一项与1的比值。但是，标尺除了缩小实际距离外，还可以扩大实际距离，使得标尺的前面项比后面项大项，然后后面的项通常变成1。作答时，只要坚持“图片上的距离：实际距离=尺度”，图片上的距离在前。

示例4.（计算地图上的距离或根据比例尺计算实际距离）

规模是

在地图上，测得 A 点和 B 点之间的距离为 2.5 厘米。 两地实际距离是多少？分析及解决方法： 方法一：比例尺为

，表示实际距离是地图上距离的60000倍。 2.5×60000=150000（厘米）

150000（厘米）= 1500 米

方法2：尺度为

，即图片上1厘米的距离代表实际距离60000厘米，即600米。 2.5×600=1500（米）

方法三：根据

= 比例尺，可以用“地图上的距离÷比例尺”或“解算比例尺”的方法求出实际距离。 2.5÷

= 2.5×60000 = 150000（厘米） = 1500 米 解：假设两地实际距离为ⅹ厘米。

1ⅹ = 2.5 × 60000

ⅹ = 150000

150000（厘米）= 1500 米

答：两地实际距离为1500厘米。

例5.（平面图形按一定比例放大后，面积扩大了比例的平方倍）

下面的大矩形是一个小矩形按比例放大得到的图。 分别测量其长度和宽度，并计算大矩形和小矩形区域的比率。

分析和解决方案：小矩形的长度为2.5 cm，宽度为1 cm； 大矩形的长度为7.5厘米，宽度为3厘米。 大矩形与小矩形的长度比为7.5：2.5 = 3：1，宽度比为3：1。

×

= 9：1 =3²：1answer：大矩形和小矩形的面积比为9：1。

示例6.（知道北部有多少位（西），向南有多少个程度（西）等）

如图所示，一辆汽车向北开车。 您能告诉购物中心和书店的汽车哪个方向？

北购物中心

45°

60º书店

0 3 6 9公里

车

分析和解决方案：从图片可以看出，将汽车作为中心，书店位于汽车的东北，购物中心位于汽车的西北。

我们如何更准确地表示他们的位置？

东北方向也被称为北部，而书店则在汽车以东的北部60º。

西北方向也称为西北方向，购物中心是汽车西北45º。

答：书店在汽车以东60º的北部60º，购物中心在汽车以西的北部为45º。

示例7.（仅当您知道对象的方向和距离时，才能确定对象的特定位置）

测量上图中从书店到汽车的距离，并根据比例计算。 这台书店在汽车以东60º的书店中有几公里？ 那购物中心呢？

分析和解决方案：从图片中，从书店和购物中心到汽车的距离分别为1.2厘米和2.3厘米。 根据量表，图片上的1 cm距离表示3公里的实际距离，并且分别计算了实际距离。

1.2×3 = 3.6（km）┄┄┄书店

2.3×3 = 6.9（km）┄┄┄购物中心

答：书店距离汽车以北60º的方向距离汽车3.6公里，购物中心距离汽车以西45º的方向为6.9公里。

注释：只有在方向词之后添加角度，才能准确地描述对象的位置。 确定方向时，您必须首先确定其是南还是向北，然后检查其是东还是西。 如果图片中没有绘制线，请先将其连接。 根据先前量表的相关知识来计算实际距离。

示例8.（歧视）书店在汽车以东的北部60º处，这意味着汽车在书店的东部也向北60º。

分析和解决方案：书店位于汽车以东60º的北部60º，汽车为中心，从北向东旋转60º； 这辆车以书店为中心，位于书店的西南，即60º在西部60º。

书店在汽车以东的北部60º，这意味着汽车在书店以西60º。

示例9.（根据给定方向和距离以有序方式确定对象的特定位置）

海上有一座灯塔。 灯塔北部和西30公里是凤凰岛。

北

西东

灯塔

0 10 20 30公里

南

您能指出图片上凤凰岛的大约位置吗？

分析和解决方案：（1）首先确定向西向北30º的方向，然后绘制射线。

30度

灯塔

（2）然后计算从地图上从灯塔到凤凰城的距离。

30÷10 = 3（cm）

凤凰岛●n

30度

灯塔

评论：在指示凤凰岛的特定位置时，您必须首先绘制指示方向的光线，然后确定从地图上从灯塔到凤凰岛的距离。 当绘制代表方向的光线时，您应该从代表灯塔的点开始，并注意正确放置量角器。

示例10.（使用方向和距离描述简单的步行路线）

下图是在某个城市的1号旅游巴士的路线图。 请根据路线图填充空白。

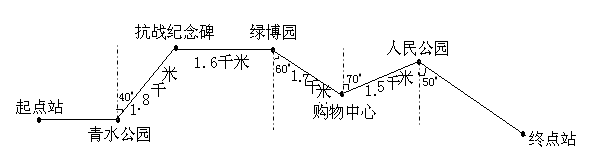
（1）1号旅游巴士从起点出发，开车到（）到Qingshui Park，然后朝（）向（）到（）（）到达反日本战争纪念碑的方向驱动（）公里。

（2）从绿色博览会公园，沿（）（）（）方向向南行走（）到购物中心，然后沿（）（）（）（）（）到达北部（）到达人民公园。

分析和解决方案：首先找到正确的方向，然后说出特定的旅程。 （1）1号旅游巴士从起点出发，前往Qingshui公园，然后在（北） - 东部（40º）方向前往反日本战争纪念碑。

（2）距南部的绿色博览会（东部）（60º）到购物中心的绿色博览会（1.7）公里，然后前往北（东）

步行（1.5）公里（70º）到达人们的公园。

评论：描述时，请确保首先清楚地说明方向，然后说明距离。 为了在谈论方向时清楚地表明，通常我们不使用东北，西北，东南，西南等术语和西北。

小学数学一般审查的解释和培训（7）

练习测试题

1.告诉以下每个量表的含义。

1∶40000

2.判断：

①小木绘制了学校操场的平面图时，他使用20厘米线的细分市场来表示地面40米的距离。

这张照片的比例为1：2。 ┈┈┈┈（）

②在特定机器零件的设计图中使用的比例为1：1。

它表明零件的实际长度与图片┈┈┈┈（）相同

③图片的刻度为6：1，此图片表示的实际距离大于图片上的距离。 ┈┈┈（）

3.选择：

①如果图纸中使用的比例小于1，那么该图（）表示的图形的距离是实际距离。

A.小于B大于C等。等于C

②学校​​游乐场长100米，宽60米。 在锻炼书中绘制图片时，更合适地将（）用作比例。

A.1：20 B.1：2000 C.1：200

4.地图上的线段的比例为。 该地图上的3厘米在实际距离中代表多少公里？

5.精度部分是图片中的12厘米，但实际长度为3毫米。 找到这张照片的比例。

6. Yinghua小学的矩形操场长120米，宽80米。 如果按比例为1：4000的计划绘制，则应在长度和宽度方面绘制多少厘米？

7.在比例为1：200000的地图上，

陈

这些城市相距5厘米。 这两个城市实际上是多少公里？ 8.地图的线段比例是：

0 40 80 120 160公里，两个城市A和B在

在此地图上，两个城市之间的距离为18厘米。 两个城市之间的实际距离是多少公里？ Bing和Ding的两个城市相距660公里。 该地图上两个城市之间的距离是多少厘米？

9.在平面图为1：500的计划视图上，矩形教室的长度测量为3厘米，宽度为2 cm。

（1）在图片和该教​​室的实际区域中找到区域。

（2）写图片上面积与实际区域的比率。 并与规模进行比较。

10.下图是1：50,000的等级图。 谈论商店，公园和电影院的位置。

电影

●30º

●●

40ºPlaza公园

●商店

（1）公园位于广场以东（）公里。

（2）电影院位于（）距离正方形的（）（）方向（）公里。

（3）商店在广场（）。

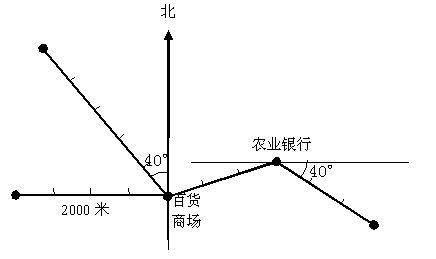
11.小敏的房屋位于百货商店以北2500米，图书馆位于中国农业银行以东1500米40度。 下面是小敏的路线图，可以从家里乘出租车到图书馆。 众所周知，在3公里以内的出租车的起跑票价（包括3公里）为9元，每增加1公里，票价将增加2元。 请根据图中提供的信息计算。 小敏在出租车票价上花了多少元？

参考答案：

1.告诉以下每个量表的含义。

1：40000表示图片上的距离是实际距离

实际距离是图的距离的40,000倍。 该图上1厘米的距离表示40,000厘米的实际距离，即400米。

图上1厘米的距离表示200公里的实际距离。

2.判断：

①当小木绘制学校操场的平面图时，它使用20厘米线的线段表示地面上的距离为40米。 这张图片的比例为1：2。┈┈┈┈（×）

②机器零件设计图的比例为1：1，表明零件的实际长度与图片上的相同。 ┈┈┈┈（√）

③图片的比率为6：1。此图片指示的实际距离大于图上的距离。 ┈┈┈（×）

3.选择：

①如果图中使用的比率小于1，则距离（a）实际距离（a）由此图片表示的图片表示。

A.小于B大于C.相等的B.

②学校​​的游乐场长100米，宽60米。 练习上的绘图更适合使用（b）作为比例。

A.1：20 B.1：2000 C.1：200

4.地图地图的线比是，此图片上的实际距离是多少公里？ 这张照片上的3厘米意味着实际距离为6公里。

5.精确零件，在图片上绘制的12厘米，实际长度为3毫米。 寻求这张图片的尺度。

图距离：实际距离=比率

12厘米= 120毫米120：3 = 40：1

答：这张照片的比率为40：1。

6. Yinghua小学有一个矩形操场，长度为120米，宽80米。 这幅画是在平面地图上以1：4000的比例绘制的。应该绘制多少厘米？

长：120米= 12000 cm 12000×

= 3厘米宽：80米= 8000 cm 8000×

= 2厘米的答案：应长3厘米，并应画2厘米。

7.在1：200000的地图上

城市和

这座城市相距5厘米，两个城市之间的距离是多少？ 5 ÷

= 1000000 cm = 10公里的答案：两个城市实际上相距10公里。

8.地图地图的线比是：

0 40 80 120 160公里，A和B的两个城市都在

该地图相距18厘米。 两个城市之间的实际距离是多少公里？ 两个城市的弯曲区相距660公里。 该地图上两个城市之间的距离是多少厘米？

18×40 = 720公里

660÷40 = 16.5厘米或66000000×

= 16.5厘米答案：两个城市之间的实际距离为720公里，这张地图上两个城市之间的距离为16.5厘米。

9.矩形教室的长度为3厘米，宽度为2厘米，平面图为1：500。

（1）找到该教室的面积和实际面积。

图面积：3×2 = 6平方厘米

实际增长：3×500 = 1500厘米实际宽度：2×500 = 1000 cm

实际面积：1500×1000 = 1500,000平方厘米= 150平方米

答：该教室的图片为6平方英尺，实际区域为150平方米。

（2）图片面积和实际面积的比率。 并与规模进行比较。

该图的面积和实际面积的比率为：6：1500000 = 1：250000

与比率1：250000 =（1：500）²进行比较

10.下图是1：5000的尺度提取的位置。谈论商店，公园和电影院的位置。

电影

●30º

●●

40园广场公园

●存储

（1）公园位于广场（0.75）公里的东部。

从公园到广场的距离为1.5厘米，1.5×50000 = 75000 cm = 0.75 km

（2）广场（北）（东）（60º）方向（0.75）公里的电影院。

（3）商店位于广场（50中的1.5公里 - 从商店到正方形的距离为3厘米

11.小米的家人位于百货商店北部的西部2500米，图书馆在农业银行农业银行以南40°的40°方向上为1,500米。 以下是小米从出租车上出租车去图书馆的路线图。 众所周知，出租车以9元（包括3公里）的起始价格为9元的起价计算，每增加1公里，它会增加2元。 请计算图中提供的信息。 小米总共花了多少出租车？

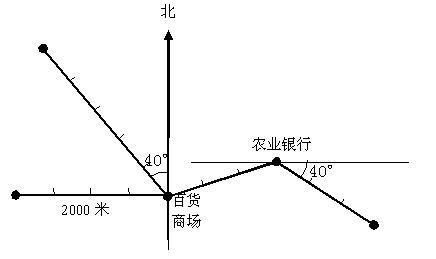
从图中的信息中可以看出，小米的房屋距离百货公司有2500米，部门商店从百货商店到农业银行和图书馆的农业银行为1,500米。 小米乘坐出租车从家里到达图书馆，总计2500 + 1500 + 1500 = 5500米，需要票价：9 + 2×（5.5-3）= 14 yuan

小学数学一般评论和培训（8）

主要内容

阳性比例和反应

学习目标

1.让学生认识到实际情况的实际情况和反比例的数量，并可以根据正比例的重要性来确定两个相关数量是正比例还是反比例。

2.使学生能够理解积极比例的图像是一条直线。 正比例关系可以给出的数据可以在方形纸上绘制相应的直线。 价值。

3.在理解比例比例和反比例的过程中，学生最初体验数量之间的相互依赖性之间的关系，并感受到有效地代表定量关系与他们的变化之间关系的不同数学模型，并进一步改善他们的思维等级。

4.让学生进一步了解数学与日常生活之间的紧密联系，增强探索数学知识和法律的意识，养成积极参与学习活动的习惯，并提高他们对学习数学的信心。

测试点分析

1.两个相关金额，一个数量变化，另一个也随之变化。 如果必须与这两个数量中的两个数字相对应的比率（即业务），则这两个数量称为正比例的数量，它们之间的关系称为正相关关系。

如果分别在字母x和y之间相关的两个数量，请使用k表示其比例，并且可以在此公式中表示阳性比例：

= k（某些）。 2.使用“描述方法”可以获得正比例图像，而正图像是直线。 在控制图像中，估计可以根据一个量的值估算与另一卷相对应的值。

3.两个相关数量，一个数量变化，另一个变化也在发生变化。 如果必须称为与这两个数量相对应的两个数字的产品，则称为反比例的数量，它们之间的关系称为抗体关系。

如果使用字母x和y之间的两个数量，并且使用k表示它们的积累，则可以在此公式中表示反比例关系：xy = k（某些）。

4.确定两个变量的比率，并且两个变量成为正比例； 必须积累两个变量的积累，并且两个变量变为反比例。 没有以上两个关系，这两个变量不是成比例的。

典型例子

示例1.（正比例的显着性）火车的时间和距离如下。 这两个数量之间有什么关系？

分析和解决方案：（1）从上表可以看出，表中有两种类型和距离。

（2）从左到右看，时间​​越来越长，旅程也扩大了； 从右到左侧，时间减少了，旅程减少了。 因此它们是两个相关的数量。

（3）旅程和时间的比率总是不变的，

= 120，

= 120，

= 120 ...这个比率是火车的速度。 通过观察和计算，我们在旅程和时间之间有两个关系：第一个点和时间是两个相关的数量，即时间变化，距离也会改变； 第二点和相应的时间比率（即速度）的比率是确定的，并且存在这种关系：

=速度（某些）。 在这两个条件下，我们可以得出结论：旅程和时间的比例比例；

评论：确定两个数量是否适当的比例，分为三个步骤：一个查看它们是否与两个数量有关； 第二个是查看一个数量的变化之一，以及另一个金额是否也更改； 它符合前两个前两个。 看看他们的比率是否确定。 不要保存任何步骤。 如果分别在字母x和y之间相关的两个数量，请使用k表示其比例，并且可以在此公式中表示阳性比例：

= k（某些）。 示例2.（确定是否为正）

锻炼的单位价格是可以肯定的。 购买练习的数量和总价是吗？ 为什么？

分析和解决方案：根据比例的重要性，请参阅两个变量的比率是否确定。 如果两个变量的比率确定，那么这两个变量将是正的，否则，这不是一个正比例。

购买练习的数量和总价为两个相关金额。 他们与实践的单位价格有以下关系：

=实践的单位价格（当然），因此实践数量和实践总价是成比例的。

示例3.（正面图像）当磁悬架列车以恒定速度行驶时，距离和时间之间的关系如下。

（1）图中的点A表示时间为1分钟，并且磁悬架序列之间的距离为7公里。 请尝试描述其他要点。

（2）连接每个点，它们在直线上吗？

（3）根据图像判断，火车运行2分钟半时，旅程是多少公里？ 行驶30公里大约需要几分钟？路线/公里

42

35

28

21

14

7●a

1 2 3 4 5 6 7时间/分钟

分析和解决方案：根据每组数据提供的数据描述图像的许多点，然后依次连接到一条直线。 相应的距离数和时间的比率为7，即，速度是确定的，距离和时间是成比例的，图像是一条直线。 在控制图像中，可以根据时间的值估算道路的值，也可以根据距离值估算时间的值。

（1）描述点和连接如图所示。

路线/公里

42●

35●

28 ●

21●●

14●

7●a

1 2 3 4 5 6 7时间/分钟

（2）在直线上，由于距离的比例和时间的比例比例，因此正比例的图像是一条直线。

（3）根据图像，当火车运行2分钟半时，旅程为17.5公里； 行驶30公里大约需要4.3分钟。

示例4.（分析）圆的周长和直径的百分比是比例的。

分析和解决方案：圆的周长和直径是比例的，但是圆的面积和半径不是正面的。

可以判断。

圆的圆和直径的相应数量为3.14，因此圆的长度和直径是成比例的。 相应数量的圆形区域和半径变化的比率变化，因此圆的面积和半径不是正的。

圆的长度和圆的直径成比例，但圆的面积和半径不是正。

示例5.（反比例的重要性）

下表是王主处理一批零件，每小时零件数量随时间变化的情况。 这两个数量之间有什么关系？

分析和解决方案：（1）从上表可以看出，每小时处理零件的数量和处理时间有两卷。 （2）从左到右，每小时处理零件的数量被扩大，并且处理时间减少； 从右到左，减少每小时处理零件的数量，并且处理时间扩大。 因此它们是两个相关的数量。 （3）每小时处理零件数量和处理时间的处理时间始终保持不变，例如20×12 = 240，30×8 = 240，40×6 = 240 ...这些批处理总数是零件的总数。

通过观察和计算，我们发现每小时的零件数量和处理时间是两个相关的数量。 相应的积累是确定的，并且存在这种关系：每小时零件的数量×处理时间=零件总数（某些）。

因此，每小时零件数量和处理时间的量是反比例的。 它们之间的关系称为反状关系。

评论：确定这两个数量是否是反比例的，并且与正相同的比例分为三个步骤：查看它们是否与两个数量有关； 第二个是看到其中一个变化，以及其他数量是否也更改； 满足前面的两个条件，然后看看他们的产品是否可以做出判断。 不要保存任何步骤。 如果使用字母x和y之间的两个相关的数量，则使用比率表示其比率，并且可以在此公式中表示正比例关系：xy = k（某些）。

示例6.（确定它是否是逆的）

总输出是确定的。 每公顷的输出和反向的公顷数量是逆的吗？ 为什么？

分析和解决方案：根据反比例的重要性，请参阅两个变量的乘积是否确定。 如果必须确定两个变量的积累，则这两个变量将成为反比例。

每公顷的输出和公顷的数量是两个相关的数量。 他们与总产出有以下关系：

每公顷产量×公顷=总输出（某些）

因此，每公顷和公顷的产量是反比例的。

示例7.（分析）和一定数量，一个加一个数量是反比例的。

分析和解决方案：确定两个变量是否相反，关键是要查看两个变量的乘积是否确定。 显然，两个加上数字的积累已更改，因此它们不相反。

而且必须，一个加一个数字，另一个没有逆转。 因为它们的积累不一定是。

评论：尽管某些相关的数量也是一种变化，而另一个数量也随之变化，但它们并非积累或不同，但它们不成比例。 还有：人的高度和高度； 某些装饰，正在减少和差异。

示例8.（综合问题1）

（1）矩形形状的面积是确定的。 为什么？

（2）矩形形状的长期长度以及长和宽度的长而宽的形式？ 为什么？

分析和解决方案：判断时，您可以在列表中列出数据，也可以根据计算公式派生。

（1）由于矩形长度×宽度的长度=矩形形状的面积（特定），所以长度和宽度是反比例的。

（2）矩形形状的长度=（长度+宽度）×2，矩形形状的长度必须，长度+宽度，并且必须为，但不可能，因此长度和宽度不相反。

示例9，（综合问题2）

在三种类型的大米中，大米的总数，千克的数量和每天吃的天数，每两个数量。

（1）肯定是米饭的总数，以及您每天吃饭的公斤和日子；

（2）您每天吃的千克数量是确定的，米饭和米饭的总数；

（3）必须确定的天数，大米的总数和每天吃的kg数量。

分析和解决方案：在总千千克的三个量中，它们每天吃的千克和几天（如果可以肯定的是一定量），其他两个数量可能会成为比例的关系或成比例的关系。 可以根据定量关系来判断它。

（1）由于您每天吃的kg数量×天数=米饭的总米（某些）（某些）千克（某些），因此，当肯定的千千克总数肯定是公斤和天数。一天中的一天是反比例的。

（2）因为

=每天（一定）进食的千克数量，因此，当您每天饮食的数量确定时，大米的总数和大米的天数是成比例的。 （3）因为

=天数（一定），因此，如果确定的天数，千千克的总数和每天的千克数量的百分比。 小学数学一般评论和培训（8）

练习测试题

1.仔细观察每种形式。 形式的两个数量之间是否存在关系？ 有什么关系？ 为什么？

表格1

表2

表3购买带有60元的笔记本电脑，笔记本的单价和可以购买的数字如下：

2.预订一批纸来练习练习书，每本书25页，您可以绑定400份。 如果要绑定500份，每个副本都带有X页。

在问题（）中，（）的量是肯定的，是关系：（）=（）=（）（）（某些），（），（）和（）和（）和（）和（）。

3.一家平方楼的瓷砖商店在客房中的侧面长度为0.3米，需要640元。 如果您使用的是0.4米长的平方砖，则需要Y。

在问题（）中，（）的量是肯定的，是关系：（）=（）=（）（）（某些），（），（）和（）和（）和（）和（）。

4.在侧面区域的三卷中，底部表面的长度和圆柱柱的高度

当底部表面的长度确定时，（）和（）to（）（）比；

当特定高，（）和（）到form（）比率时；

当侧面区域确定时，（）to（）to form（）比率。

5.在分裂，分裂和业务的三个数量中，

当（）当然，（）和（）成为正式比例；

当（）当然，（）和（）成为反比例；

6.当A×B = C（A，B，C为三个量，而不是0）。

（）必须，（）和（）to form（）比率;

（）必须，（）和（）to form（）比率;

（）必须，（）和（）to form（）比率;

7.判断。

（1）确定的总数是确定的，工作效率和工作时间的比例是逆的。 ( )

（2）图片上距离和实际距离之间的距离。 ( )

（3），x和y代表两个变化的数量，同时5x -7y = 0，x和y不成比例。 ( )

（4）得分的大小是确定的，其分子和脱词是成比例的。 ( )

（5）在一定距离的情况下，车轮周长及其旋转的旋转次数是反比例的。 ( )

（6）两个相关的数量不是正的，并且成为一个反比例。 ( )

（7）订阅“小学数学评估手册”。 ( )

（8）在400级赛车中，跑步速度和以上比率使用的时间。 ( )

（9）确定的总工作量，完整的数量和未完成的卷是反比例的。 ( )

（10）立方体的长度和体积是比例的。 ( )

（11）划分是确定的，该划分为反比例。 ( )

（12）圆的周长及其直径为正。 ( )

8.确定每个问题中的两个数量是否成比例。

（1）配备了一批电视，每天组装桌子数量和所需的天数（）。

（2）正方形的侧面长度和情况（）。

（3）池的体积是可以肯定的。

（4）房间的面积确定，每个砖块的面积和砖块的数量（）。

（5）在一定时间内，每个部分（）中使用的时间数和处理零件的数量。

（6）在一定时间内，每小时处理零件的数量和处理零件的数量（）。

9.思考：显然在三岁和44公斤的年龄在11岁时12公斤。 因此，张张说：“显而易见的重量是正面的正面。” 您认为张张说对吗？ 为什么？

10.造纸厂中有多少吨造纸是每小时1.5吨，2小时3小时？

（1）填写下面的表完整。

（2）根据表中的数据，造纸时间的点以及下图中的纸张数量，然后将它们连接。

1 2 3 4 5 6 7时间/h

（3）造纸的数量和造纸的时间比例是吗？ 为什么？

（4）根据图像判断，在5小时内有多少吨造纸？

参考答案：

1.仔细观察每种形式。 形式的两个数量之间是否存在关系？ 有什么关系？ 为什么？

表格1

= 4，

= 4，

= 4 ...因为

=单价（一定），因此，如果确定单位价格，总价格和数字是正确的。 表2

= 4，

= 4，

= 4 ...因为

=数量（某些），因此，如果确定数量，总价格和单位价格是比例的。 Table 3 Buy a laptop with 60 yuan, the unit price of the notebook and the number that can be purchased are as follows:

1.5 × 40 = 60, 2 × 30 = 60, 4 × 15 = 60 ...

Because the unit price × quantity = total price (certain), when the total price is certain, the unit price and the quantity are inverse.

2. Booking a batch of paper to practice the exercise book, 25 pages per book, you can bind 400 copies. If you want to bind 500 copies, each with a X page.

In the question (the total number of paper) (the total page of the paper), the relationship: (number of each page) × (the number of binding books) = (total number of paper) (certain), (each page number), (each binding number) becoming (Anti -) ratio.

3. A square floor tile shop with a side length of 0.3 meters in a guest room requires 640 yuan. If you use a square floor tile with a side length of 0.4 meters, you need Y.

In the question (the area area of ​​the guest room), the amount of the relationship is certain, the relationship formula: (the area of ​​each brick) × (the number of bricks) = (the area area of ​​the guest room) (certain), (the area of ​​each brick) and (brick of the brick) and (brick of the brick) Blocks) (reverse) ratio.

4. Among the three volumes of the side area, the length of the bottom surface, and the height of the cylindrical pillar

When the length of the bottom surface is certain, (side area) to (high) form (positive) ratio;

When height is certain, (side area) and (long -sided) ratio (positive) ratio;

When the side area is certain, the proportion of (high) to (high) (high) (reverse) ratio.

5. Among the three quantities of being divided, divisive, and business,

When (divide) certainly, (divide) and (quotient) are proportional;

When (divide) certainly, (divide) and (quotient) inverse proportion;

6. When A × B = C (A, B, C is three quantities, and it is not 0).

(C) must, (A) to (b) to form (reverse);

(A) must, (C) to (B) to form (positive) ratio;

(B) must, (C) to (a) form (positive) ratio;

7. Judgment.

(1) The total amount of work is certain, and the proportion of work efficiency and working time is inverse. (√)

(2) The distance between the distance and the actual distance on the picture. (×)

(3), x and y represent the amount of two changes, at the same time 5x -7y = 0, x and y are not proportional. (×)

(4) The size of the score is certain, and its molecules and denominates are proportional. (√)

(5) In a certain distance, the wheel perimeter and the number of rotations it rotate are inverse proportion. (√)

(6) The two associated quantities are not positive, and it becomes an inverse proportion. (×)

(7) Subscribe to the "Elementary School Mathematics Evaluation Manual". (√)

(8) In the 400 -meter racing, the speed of running and the time used to be used in the inverse ratio. (√)

(9) The total amount of work is certain, and the completed amount and the unfinished volume are inverse proportions. (×)

(10) The length and volume of the cube are proportional. (×)

(11) The division is certain, and the division is to the inverse proportion. (√)

(12) The perimeter of the circle and its diameter are positive. (√)

8. Determine whether the two quantities in each question are proportional.

(1) Equipped a batch of TVs, assembled the number of desks to the number of days (inverse).

(2) The side length of the square and the length (positive ratio).

(3) The volume of the pool is certain, and the amount of water injection and time (reverse) used for water pipes per hour.

(4) The area of ​​the room is certain, and the area of ​​each brick and the number of blocks (inverse).

(5) In a certain period of time, the time used to process each part and the number of processing parts (inverse proportions).

(6) In a certain period of time, the number of processed parts per hour and the number of processing parts (proportions).

9. Thinking: Obviously 12 kg at the age of three and 44 kg at the age of eleven. So Xiao Zhang said, "Obvious weight to be positive with height." Do you think Xiao Zhang said right? 为什么？

Answer: Xiao Zhang's saying is wrong. Weight and height are not two associated amounts. The weight and height are not proportional.

10. How many tons of papermaking in a paper mill is 1.5 tons per hour, 2 hours, 3 hours?

(1) Fill in the table below complete.

(2) According to the data in the table, the point of the papermaking time and the number of tons of paper in the figure below, and then connect them.Ton number/ton

6 ●

3●

1 2 3 4 5 6 7 time/h

(3) Is the number of tons of papermaking and the time proportion of papermaking? 为什么？

因为

= The number of tons of paper per hour (certain), so when the number of tons of paper per hour is certain, the number of tons of papermaking is proportional to the papermaking time. (4) How many tons of papermaking in 5 hours according to the image judgment?

According to image judgment, 5 hours of papermaking 7.5 tons