人教版数学六年级下册第三单元知识点＋核心考点+同步练习+测试卷5套含答案

六年级

第一单元知识点

六年级

第二单元知识点

六年级

第三单元知识点

第三单元知识点

1.气缸的认识

圆柱体的特征： 圆柱体由两个底面和一个侧面包围。 它的底面是两个大小相同的圆，侧面是一个曲面。 柱的边沿高度展开，形成矩形（或正方形）。 这个长方形（或正方形）的一条边的长度等于柱底的周长，另一边的长度等于柱的高度。

圆柱体的高度：圆柱体两个底面之间的距离称为高度。 圆柱体有无数个高度。

2.圆柱体的表面积

圆柱体的侧面积：圆柱体的侧面积=底周长×高

用字母表示为S方=Ch

圆柱体表面积：圆柱体表面积=边面积+底面积×2

用文字表示为 S = 2πrh + 2πr2

3、气缸容积

含义：圆柱所占空间的大小称为圆柱的体积。

圆柱体体积计算公式：圆柱体体积=底面积×高

用字母表示为V=Sh

4. 锥体的理解

圆锥体的特征：圆锥体由底面和侧面包围。 它的底面是圆形，侧面是曲面。

圆锥体的高度：从圆锥体的顶点到底面中心的距离就是圆锥体的高度。 锥体只有 1 巴高。

5. 圆锥体积

圆锥体的体积等于同底同高的圆柱体体积的1/3。

圆锥体体积计算公式：圆锥体体积=底面积×高×1/3

用字母表示为 V 锥 = 1/3 Sh

人民教育出版社六年级版第二册第三单元同步习题及答案

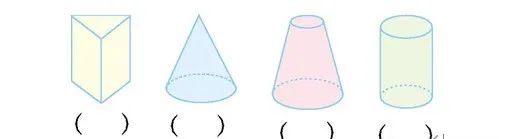
1、下图中，圆柱体画“√”，圆锥体画“○”。

2. 填空。

1、圆柱和圆锥的底面积和体积相等。 圆柱体的高度为 12 分米，圆锥体的高度为 ( ) 分米。

2、将一个体积为24立方厘米的圆柱体切成最大的圆锥体。 去除部分的体积为( )立方厘米。

3、圆柱体的侧面展开图是边长为12.56分米的正方形。 圆柱体底面直径为 ( ) 分米，高为 ( ) 分米。

4、圆柱体底面直径扩大为原来的2倍，高度不变，侧面积扩大为原来的()倍，体积扩大为原来的()倍。

5. 圆锥体的底周长为 6.28 厘米，高为 15 厘米，体积为 ( ) 立方厘米。 同底同高的圆柱体的体积是（ ）立方厘米。

6、将一块长4米的圆柱木锯成两块圆柱后，表面积增加1.2平方米。 这块圆柱形木头的体积是（ ）立方米。

7. 圆锥体的体积为 8 立方分米，底面积为 2 平方分米，高为 ( ) 分米。

8、圆柱体和圆锥体同底同高，体积差40立方厘米。 圆柱体的体积为 ( ) 立方厘米，圆锥体的体积为 ( ) 立方厘米。

3.判断题。 （正确则画“√”，错误则画“✕”）

1.圆锥体的底面是椭圆形。 ( )

2.长方体、正方体、圆柱体、圆锥体的体积可以用“底面积×高”计算（ ）

3、当圆柱体底面周长等于高度时，沿一定高度切割，其边长展开为正方形（ ）

4. 两个表面积相等的圆柱体不一定具有相等的体积 ( )

5. 圆锥体的底径和高度均为 4 分米。 如果沿底径切成两半，表面积将增加 8 平方分米 ( )

4.多项选择题。 （将正确答案的数字填在括号内）

1. 求一个圆柱形水桶能装多少水，就是求水桶的（）。

A. 侧面区域

B.表面积

C、体积

D、底部区域

2、如果圆柱体的高度保持不变，而底面半径扩大到原来尺寸的2倍，则其体积将扩大到原来尺寸的()倍。

A.4

B.8

C.12

D.16

3. 将一块木头加工成最大的圆柱体。 其底座直径为10厘米。 这个立方体的体积是()立方厘米。

A.8000

B.4000

C.1000

D.314

4.24 相同的圆锥形实心铁块可以熔化并铸造成与其底面和高度相同的()圆柱形实心铁块。

A.4

B.8

C.12

D.72

5. 计算下图的体积。 （单位：厘米）

6.解决问题。

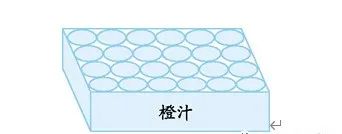
1、橙汁罐为圆柱形，底径6厘米，高11厘米。 将24罐橙汁放入一个盒子中。 盒子的长、宽、高分别是多少厘米？

2、圆柱形钢材长3米，横截面直径2厘米，每立方厘米钢重7.8克。 这块钢重多少克？

3、圆柱形机械零件的底部直径为3厘米，高度为0.4厘米。 如果这个零件的表面是喷漆的。 需要涂漆的面积是多少平方厘米？

4、打谷场上有一个近似圆锥形的麦堆。 实测底部周长9.42米，高1.2米。 每立方米小麦重约750公斤。 这堆小麦重多少公斤？ （精确到最接近的公斤）

5. 一根圆柱形钢管长100厘米，外半径为4厘米，内半径为3厘米。 这根钢管的体积是多少？

6、将长度为12厘米、截面半径为3厘米的圆柱形钢坯浇铸成底面半径为6厘米的圆锥形钢坯。 圆锥形坯料的高度是多少厘米？

参考答案

1.()(○)()(√)

2.1.362.163.412.564.245.15.747.1

6.2.47.128.6020

3.1.✕2.✕3.√4.√5.✕

4. 1.C2.A3.C4.B

5. 376.8立方厘米 502.4立方厘米

6. 1. 长：6×6=36（厘米） 宽：4×6=24（厘米）

高度：11厘米

2.3.14×(2÷2)2×(3×100)×7.8=7347.6（克）

3.3.14×(3÷2)2×2+3.14×3×0.4=17.898（平方厘米）

4.9.42÷3.14÷2=1.5(米)

3.14×1.52×1.2×750≈2120(公斤)

5.3.14×(42-32)×100=2198（立方厘米）

6.3.14×32×12×3÷(3.14×62)=9(厘米)

人民教育出版社六年级第二册第三单元测试题及答案1

参考答案

套装2

小学六年级卷2

第三单元 跟踪检测纸

圆柱体和圆锥体

1. 填写。 （每空格2分，共30分）

1. 圆柱体的底面直径为15厘米，高为8厘米。 圆柱体的边面积为()cm2。

2、沿底座直径纵向切割圆锥体，切割面呈（）形。

3． 如图所示，圆柱形玩具的侧面有一块装饰布。 圆柱体底部半径为10厘米，高为18厘米。 当装饰布展开时，它变成一个长方形，长为()厘米，宽为()厘米。

4、如图所示，一根底径为20厘米、长为50厘米的圆柱形通风管沿地面滚动一圈，滚动的面积为()cm2。

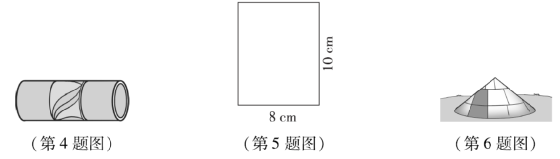
5、如图所示，以长方形的10厘米长边的直线为轴旋转，会得到一个（），它的表面积为（）cm2，体积为（）cm3。

6. 近似圆锥形的露营帐篷（如上图所示），底半径为3米，高为2.4米。 帐篷的面积是()平方米，容纳的空间是()。

7、如图所示，将直角三角形以6厘米长的直角边为轴，绕直线旋转一周。 所得数字为（），其体积为（）cm3。

8. 上图是一个用纸板制成的圆柱形蛋糕盒。 底部半径为 10 厘米，高度为 12 厘米。 用丝带包裹这个蛋糕盒。 至少需要 () 厘米的丝带。 （用约20cm的丝带打结）

9. 圆柱体和圆锥体具有相同的底和高。 若圆柱体的体积比圆锥体的体积大42dm3，则圆柱体的体积为()，圆锥体的体积为()。

2.区分一。 （正确答“√”，错误答“×”）（每题2分，共10分）

1.圆锥体的体积比圆柱体的体积小23。 ()

2、如果圆锥底面积不变，高度扩大到6倍，体积就会扩大到2倍。 ()

3． 圆柱体的侧视图一定是长方形。 ()

4、圆柱体底座直径为3厘米，高为9.42厘米。 它的边沿高度扩展，形成一个正方形。 ()

5. 圆柱体有无数个高度，而圆锥体只有一个高度。 ()

3. 选择一项。 （括号内填入正确答案数）（每题2分，共10分）

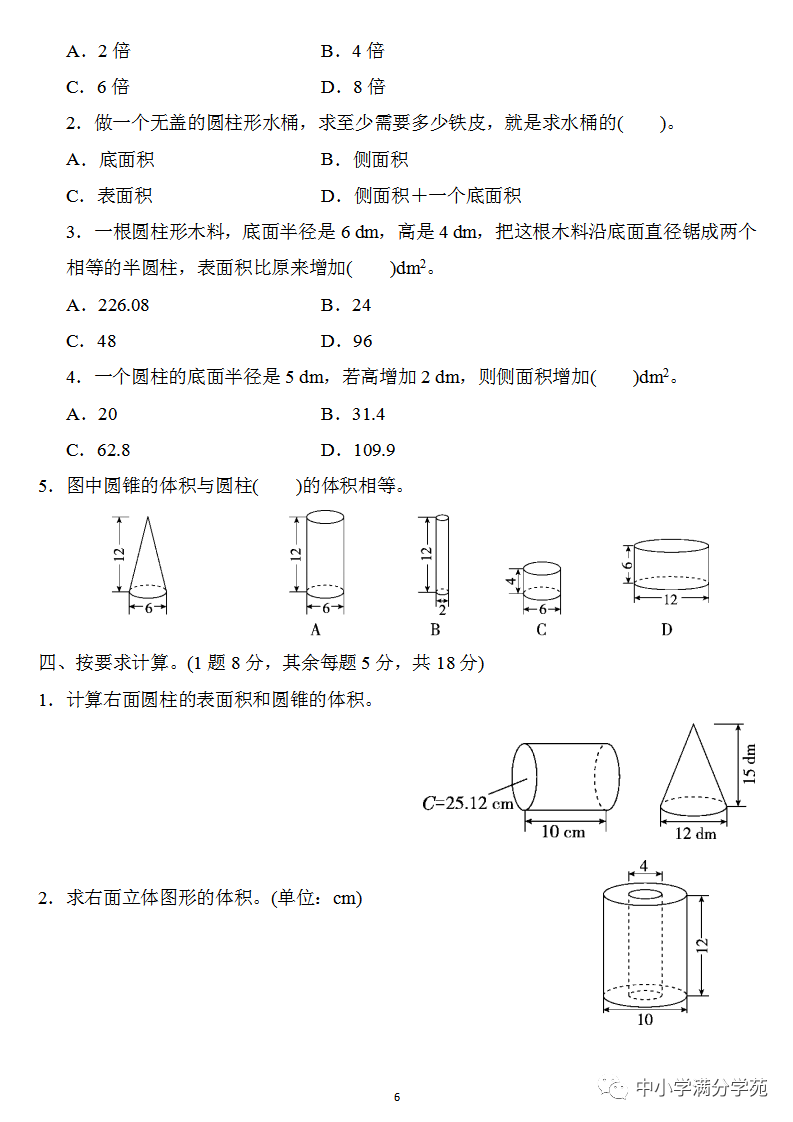
1. 如果圆柱体的底半径和高度扩大到原来尺寸的两倍，则其体积将扩大到原来尺寸（）。

A. 2 次 B. 4 次 C. 6 次 D. 8 次

2、制作一个没有盖的圆柱形水桶，求最少需要的铁皮数，即求出水桶的（）。

A. 底面 B. 侧面区

C. 边区 + 两个底区 D. 边区 + 底区

3． 一块圆柱形木头的底面半径为 6 分米，高度为 4 分米。 这块木头沿着底径被锯成两个相等的半圆柱体。 表面积比原来增加()dm2。

A.226.08 B.24C． 48 D． 96

4. 圆柱体的底面半径为 5 dm。 如果高度增加2dm，则侧面面积增加()dm2。

A.20 B. 31.4℃。62.8D。 109.9

5、图中圆锥体的体积等于圆柱体()的体积。

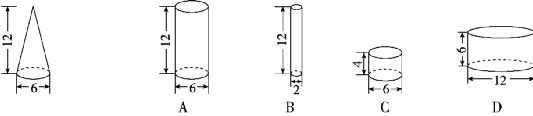
4.我会按照要求正确回答问题。 （每题6分，共18分）

1.求下图中圆柱体的表面积。

2.你能求出它的体积吗？

3． 求下图中空心圆柱体的体积。 （单位：厘米）

5、走进生活，解决问题。 （第4题和第5题各7分，其余各题6分，共32分）

1、下图中的“博士帽”是纸板做的（除了流苏）。 上部为边长30厘米的正方形，下部为底径18厘米、高8厘米的圆柱体，无盖无底。 制作100顶这样的“医生帽”，需要多少平方分米的纸板？

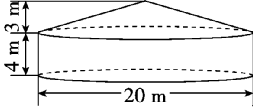
2、牧民搭建的蒙古包如图所示。 这个蒙古包的体积是多少立方米？

3． 一块圆柱形木头长 30 分米，底径为 4 分米。 将其分成3个相等的圆柱体后，表面积增加了多少平方分米？

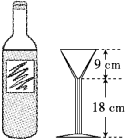
4、酒瓶中酒的高度正好等于锥形高脚杯的高度（如图）。 据了解，酒瓶底部内径为8厘米，高脚杯顶部内径也为8厘米。 如果将瓶子里的酒全部倒入高脚杯中，可以倒入多少杯酒？

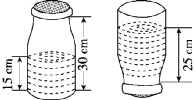
5、如图所示，奶瓶深30厘米。 从内部测量底部的直径为10厘米。 牛奶在瓶子里的深度是15厘米。 将瓶口塞紧后，将其倒置，瓶口朝下。 此时牛奶的深度为25厘米。 体积是多少毫升？

回答

1.1.376.82。 等腰三角形 3.62.8184.3140

5. 圆柱形 904.322009.6

[点击] 旋转后，8厘米成为圆柱体的底半径。

6.28.2622.608立方米[呼叫]别忘了带上设备。

7. 锥体 25.128.1489.63 dm321 dm3

2.1.×2.×3.×4.√5.√

3. 1.D2.D3.D4.C5.C

4. 1.25.12÷3.14÷2＝4(厘米)

25.12×10＋42×3.14×2＝351.68(cm2)

2.12÷2＝6(分米)

3.14×62×15×13＝565.2(dm3)

3.10÷2＝5(厘米)

4÷2＝2(厘米)

3.14×52×12-3.14×22×12＝791.28(cm3)

5、1.1顶部：3.14×18×8＋30×30＝1352.16(cm2)

100条：1352.16×100＝135216(cm2)＝1352.16(dm2)

答：至少需要 1352.16 dm2 的纸张。

【使用说明】紧扣“无盖无底”关键词，注意单位变化。

2.20÷2＝10(米)

3.14×102×4+3.14×102×3×13

＝1256＋314＝1570(立方米)

答：这个蒙古包的体积是1570立方米。

3.4÷2＝2(dm)3.14×22×4＝50.24(dm2)

答：表面积增加了 50.24 dm2。

4、方法一：3.14×(8÷2)2×(18+9)÷[3.14×(8÷2)2×9×13]=9（杯）

方法二：（18＋9）÷9×3＝9（杯）

答：可以装9杯。

5.3.14×(10÷2)2×(30-25+15)＝1570(cm3)＝1570(mL)

答：奶瓶的容量是1570毫升。

套装3

1、下图中，圆柱体画“√”，圆锥体画“○”。

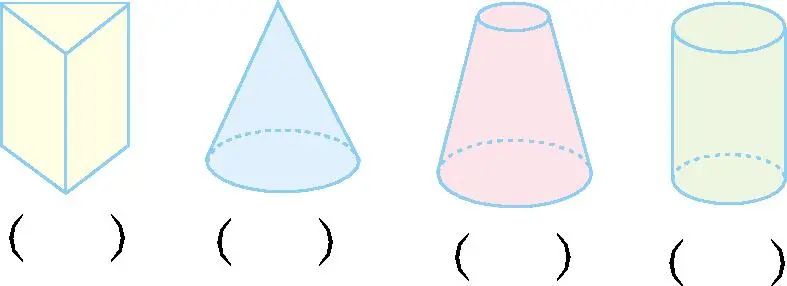
2. 填空。

1、圆柱和圆锥的底面积和体积相等。 圆柱体的高度为12分米，圆锥体的高度为()分米。

2、将一个体积为24立方厘米的圆柱体切成最大的圆锥体。 除去部分的体积为()立方厘米。

3、圆柱体的侧面展开图是边长为12.56分米的正方形。 这个圆柱体的底面直径是()分米，高是()分米。

4、圆柱体底面直径扩大为原来的2倍，高度不变，侧面积扩大为原来的()倍，体积扩大为原来的()倍。

5、圆锥体的底周长是6.28厘米，高是15厘米，体积是()立方厘米。 同底同高的圆柱体的体积是()立方厘米。

6、将一块长4米的圆柱木锯成两块圆柱后，表面积增加1.2平方米。 这块圆柱形木头的体积是()立方米。

7.圆锥体的体积为8立方分米，底面积为2平方分米，高为()分米。

8. 圆柱体和圆锥体的底和高相同，体积差为 40 立方厘米。 圆柱体的体积为()立方厘米，圆锥体的体积为()立方厘米。

3.判断题。 （正确则画“√”，错误则画“✕”）

1.圆锥体的底面是椭圆形。 ()

2.长方体、正方体、圆柱体、圆锥体的体积可以用“底面积×高”计算。 ()

3、当圆柱体底面周长等于高度时，沿一定高度切割，其边长展开为正方形。 ()

4. 两个表面积相等的圆柱体不一定具有相等的体积。 ()

5. 圆锥体的底径和高度均为 4 分米。 如果沿底径将其切成两半，表面积将增加8平方分米。 ()

4.多项选择题。 （将正确答案的数字填在括号内）

1. 求一个圆柱形水桶能装多少水，就是求水桶的（）。

A. 侧面面积 B. 表面积 C. 体积 D. 底部面积

2、如果圆柱体的高度保持不变，而底面半径扩大到原来尺寸的2倍，则其体积将扩大到原来尺寸的()倍。

A.4B.8C.12D.16

3. 将一块木头加工成最大的圆柱体。 其底座直径为10厘米。 这个立方体的体积是()立方厘米。

A.8000 B.4000C.1000D.314

4.24 相同的圆锥形实心铁块可以熔化并铸造成与其底面和高度相同的()圆柱形实心铁块。

A.4B.8C.12D.72

5. 计算下图的体积。 （单位：厘米）

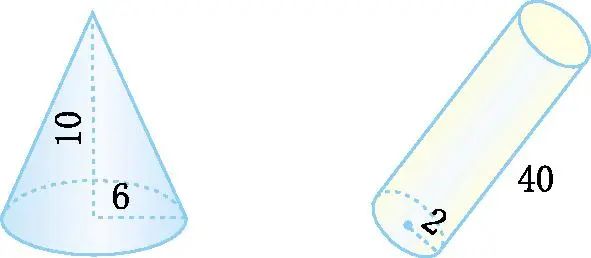
6.解决问题。

1、橙汁罐为圆柱形，底径6厘米，高11厘米。 将24罐橙汁放入一个盒子中。 盒子的长、宽、高分别是多少厘米？

2、圆柱形钢材长3米，横截面直径2厘米，每立方厘米钢重7.8克。 这块钢重多少克？

3、圆柱形机械零件的底部直径为3厘米，高度为0.4厘米。 如果这个零件的表面是喷漆的。 需要涂漆的面积是多少平方厘米？

4、打谷场上有一个近似圆锥形的麦堆。 实测底部周长9.42米，高1.2米。 每立方米小麦重约750公斤。 这堆小麦重多少公斤？ （精确到最接近的公斤）

5. 一根圆柱形钢管长100厘米，外半径为4厘米，内半径为3厘米。 这根钢管的体积是多少？

6、将长度为12厘米、截面半径为3厘米的圆柱形钢坯浇铸成底面半径为6厘米的圆锥形钢坯。 圆锥形坯料的高度是多少厘米？

参考答案

套装 4

附上第 3 单元的练习

1. 填空。

1. 圆柱体的高度为（ ）； 圆锥体的高度为 ( )。

2. 将圆柱体的侧面沿（ ）线剪开，展开后得到一个长方形。 该矩形的长度等于圆柱体 ( )，宽度等于圆柱体 ( )。

3. 有一个底半径为2cm、高为5cm的圆柱体。 其侧面积为( )，表面积为( )，体积为( )。

4、圆柱体的边面积为188.4m2，高为10m，底面积为( )，体积为( )。

5、边长6dm的方形纸形成圆柱形纸管（接头不计）。 该纸管的边面积为 ( )

6. 圆柱体和圆锥体具有相同的底和相同的高度。 圆柱体的体积为 90 厘米，则圆锥体的体积为 ( ) 立方厘米。

7. 将底径为 2dm、高为 3dm 的圆柱体切成最大的圆锥体，并除去 ( ) 立方分米。

8. 一块圆柱形木头长20分米。 如果将其切成4个相同的部分，则表面积增加18.84平方分米。 圆柱木切削后每段的体积为（ ）。

9. 圆柱体和圆锥体底高相同，体积差8厘米。 圆锥体的体积为 ( ) 立方厘米。

10. 已知两个圆柱体的高度相等，底半径之比为1：2，则它们的体积比为（ ）。

11. 等底等高的圆柱体和圆锥体，其体积之和为 64dm，圆柱体的体积为 ( )，圆锥体的体积为 ( )。

12、制作一根底径为20厘米、长度为60厘米的圆柱形通风管，至少需要( )平方厘米的铁皮。

13、如右图所示，将一个直径为4厘米，高为10厘米的圆柱体，沿底座直径均匀分成几份，然后将圆柱体切割并拼成一个近似长方体，和它一样高和高。 长方体的表面积比圆柱体的表面积大( )平方厘米。

14、将一个圆锥体浸入盛有水、底面积为30cm2的圆柱形容器中。 水面上升4厘米。 圆锥体的体积为 ( ) 立方厘米。

2. 选择一项。 （选择正确的答案数并填入括号）

1. 将一段圆柱形钢块切成最大的圆锥体。 拆下的部分重8公斤。 此段圆钢重（ ）公斤。

A.12 B.8 C.24

2. 将圆柱体的边沿高度展开，得到边长为 4dm 的正方形。 这个圆柱体的边面积是( )平方分米。

A.16 B.50.24 C.100.48

3、用一张正方形纸拼成一个圆柱体（接口忽略），这个圆柱体的（ ）相等。

A. 底部直径和高度 B. 底部周长和高度

C.底部区域和侧面区域

4. 圆柱体的底面半径为5分米。 如果高度增加 2 分米，则侧面面积增加 ( ) 平方分米。

A.31.4 B.20

C.62.8 D.109.9

5. 将圆柱形橡皮泥球揉成与它同底的圆锥体，高度 ( )。

A. 扩大 3 倍 B. 缩小 3 倍 C. 扩大 6 倍

6. 比较等底等高的圆柱体、正方体、长方体的体积，（ ）。

A. 立方体的体积很大。 B、长方体的体积很大。

C. 圆柱体的体积较大 D. 尺寸相同

3、判断。

1、圆柱体的体积与圆锥体的体积之比为3：1。 ( )

2.圆锥的底面积保持不变。 如果高度增加三倍，体积也会增加三倍。 ( )

3. 如果两个圆柱体的边面积相等，则它们的体积也相等。 ( )

4、圆柱体底座直径为3厘米，高为9.42厘米。 沿高度剪开，其边将展开为正方形。

( )

5、半径为2dm的圆柱体，其底周长和底面积相同。 ( )

4.图形和计算。

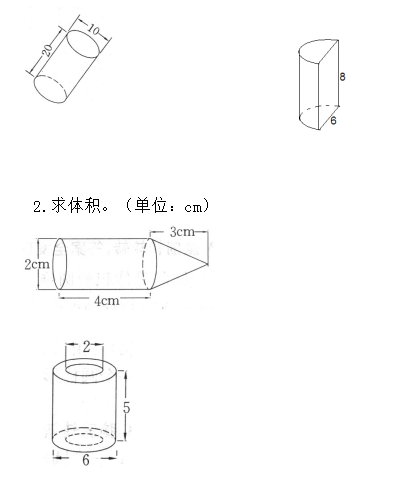
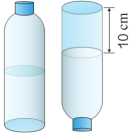
5、解决问题。

1、装满一瓶矿泉水。 红红喝了一些。 拧紧盖子并将其倒置。 无水部分高度为10cm，内径为6cm。 红红喝了多少水？

2、底部直径30米、深2.5米的圆柱形游泳池。

(1)经线内壁及底面涂抹水泥。 胶结部分的面积是多少平方米？

(2) 将游泳池注满水，使水深为水池深度的 5(4)。 应该加多少立方米的水？

3、圆锥形黄沙堆底周长25.12m，高1.5m。 每立方米黄沙重1.5吨。 这个黄沙锥重多少吨？

4、小刚家有一个圆柱形鱼缸。 从内部测量底部直径为30厘米。 爸爸把珊瑚放进鱼缸里（全部浸在水里，没有水溢出）。 水面由原来的25厘米上升到28厘米。 请计算一下珊瑚的数量。 音量是多少？

5、压路机前轮为轮宽2m、直径1.2m的圆筒。 如果它旋转5次，总共会覆盖多少平方米的道路？

6、卡车箱体为长方体，长4m，宽1.5m，高4m。 它装满了一卡车沙子。 卸完后，砂子堆成高2m的圆锥体。 它的基地面积是多少？ 平方米？

套装 7

▍编辑：唐山家庭教育网