弹性模量线的选择对钢材屈服强度Rp0.2测量值的影响

高强度钢

高强度钢是指采用微合金化和热机械轧制技术生产的具有高强度（强度等级≥460MPa）、良好塑性、韧性和加工性能的结构钢。 广泛应用于桥梁、建筑、长输管道、汽车等领域。 和其他领域。 高强度钢材的使用可以减小构件尺寸和结构重量，相应地降低建筑成本并创造更大的净使用空间。 近年来，中国、美国、欧洲、日本等地的桥梁工程、建筑结构、输电铁塔等钢结构工程中越来越多地采用高强钢。

高强度钢是连续屈服材料，屈服强度无法测量。 非比例延伸强度需要测量为其屈服强度。 当样品尺寸和温度确定后，影响样品屈服强度Rp0.2测量结果的因素主要包括力值误差、引伸计误差、截面积测量精度、实际拉伸应变率和试验结果。 这样的夹紧条件等。

GB/T 228.1-2010《金属材料拉伸试验第1部分：室温试验方法》规定，在应力-应变曲线上，画一条与曲线弹性直线段平行的线（以下简称弹性模量）线）并延伸 到轴上该直线段的距离是一条等于 0.2% 伸长率的直线。 该平行线与曲线的交点对应的强度为Rp0.2。 然而，很多情况下应力-应变曲线的弹性模量线并不完全是直线，这使得Rp0.2难以准确测量。 笔者从不同的拉力测试实验室了解到，目前的拉力试验机都有试验机程序，测试时软件会自动计算Rp0.2。 但由于不同试验机软件中弹性模量线的选择方法不同，导致结果弹性模量线与实际应力应变曲线拟合程度略有差异，从而影响了弹性模量线的斜率mE的值。模数线，进而影响Rp0.2的测量值。

笔者选取拉伸曲线上屈服现象明显的Q235B碳素结构钢和连续屈服的DP780高强钢进行室温拉伸试验。 为了避免其他因素对试验结果的影响，两种材料均在某型拉力试验机上进行了拉力试验。 拉伸试验完成并确定载荷和变形数据后，选择不同的弹性模量线重新进行试验。 计算并观察应力-应变曲线弹性模量线部分的拟合程度，得到不同的mE和对应的Rp0.2，研究弹性模量线的选择对Rp0.2实测值的影响。

样品制备和测试方法

样品制备

试验材料为某公司生产的6mm厚Q235B碳素结构钢和2mm厚DP780高强钢。 横向拉伸试样按GB/T 228.1-2010制备。

实验方法

在室温23℃下，用精度符合要求的千分尺测量试件的横截面积。 将制备好的拉伸试样按照GB/T 228.1-2010中方法A在某型号试验机上进行试验。 试验后，得到弹性模量线mE的斜率和屈服强度Rp0.2。 将应力应变曲线的0%～2%拉应变部分放大，得到弹性模量线拟合图，观察拟合程度。

弹性模量线的选择

试验机以50Hz的频率采集数据。 同时通过测力仪、梁位移、引伸计每0.02秒采集一次载荷、位移、变形数据。 通过后台计算截面积，可以实时得到应力应变拉伸曲线。 测试完成后，系统根据预设的方法获取弹性模量线，从而得到相应的修正原点和Rp0.2。

笔者在试验机上选取了以下两种弹性模量线预设方法进行计算。

（1）自动杨氏模量：系统选择最大载荷的2%到最大载荷（自动确定上下屈服，有屈服则选择上屈服）作为弹性模量选择区间，并根据下式计算其斜率：最小二乘法。 ，得到我。

(2)杨氏模量：人为选择起始点和终点作为弹性模量选择区间，根据最小二乘法计算斜率，得到mE。

这次载荷和变形数据确定后，作者将计算Rp0.2的默认自动杨氏模量改为3个不同的应力区间，分别得到了4个不同的mE和对应的Rp0.2，并截取了0%到2 %拉伸应变曲线，观察弹性模量线与曲线弹性截面的拟合情况。 为了消除开始时的非线性阶段，选择起始点的拉应力为30MPa，根据曲线形状和抗拉强度值选择终点。

测试结果与讨论

检测结果

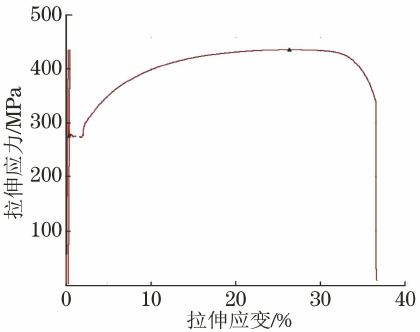
图1 Q235B碳素结构钢的应力应变曲线

图2 DP780高强钢的应力应变曲线

从图1和图2可以看出，Q235B碳素结构钢在4种条件下的4 Rp0.2均在拉伸应变0.3%~0.4%之间，而DP780高强度钢在4种条件下的4 Rp0.2条件 拉伸应变均在 0.4% 至 0.5% 之间。 表1显示了拉伸试验结果。

表1 拉伸试验结果

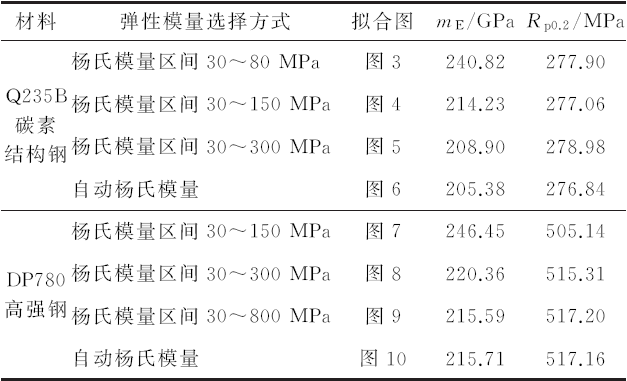
分析与讨论

Q235B碳素结构钢结果分析

从图1可以看出，Q235B碳素结构钢的拉伸曲线有明显的上下屈服。 屈服强度上限为297.57MPa，抗拉强度为435.25MPa，自动杨氏模量范围为8.7~297.57MPa。 。

从表1可以看出，弹性模量线的选择方法对mE有直接影响，但对Rp0.2影响不大。 当弹性模量选择区间终点为80MPa时，mE明显偏大，达到240.82GPa； 弹性模量选择区间的终点越接近拉伸强度，则mE值越接近自动杨氏模量的mE值。 当大于抗拉强度mE时，无法获得抗拉强度Rp0.2。

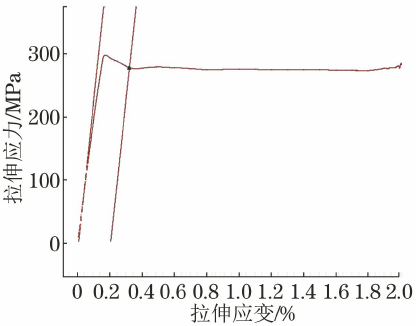
图3 Q235B碳结构钢的应力应变曲线（选取杨氏模量30~80MPa）

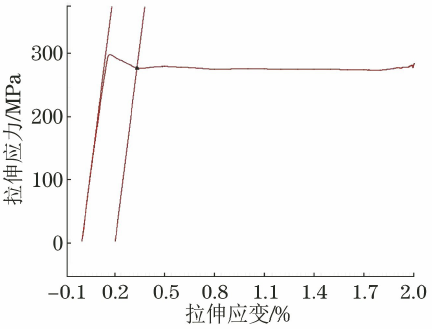
图4 Q235B碳结构钢应力应变曲线（选取杨氏模量30~150MPa）

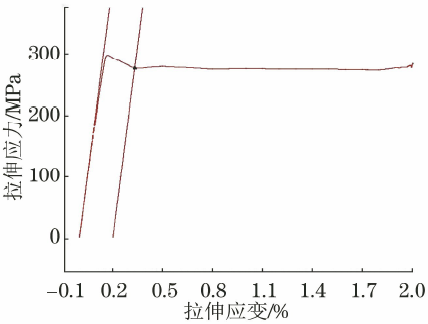
图5 Q235B碳结构钢应力-应变曲线(选取杨氏模量30~300MPa)

图6 Q235B碳结构钢的应力应变曲线（自动杨氏模量）

从图3~图6可以看出，当弹性模量选择区间终点为80MPa时，弹性模量线与曲线弹性段拟合程度较差，导致mE值明显偏大。 由于Q235B碳素结构钢有明显的上下屈服，在屈服平台上，0.3%~0.4%应变值对应的应力值相差不大，因此较大的mE值并不会导致明显的差异。 Rp0.2 值。

DP780高强度钢结果分析

从图2可以看出，DP780高强钢的拉伸曲线呈现连续屈服现象，拉伸强度值为854.38MPa，本次自动杨氏模量范围为17~854.38MPa。

从表1可以看出，弹性模量线的选择方法对mE有直接影响，对Rp0.2有显着影响。 当弹性模量选择区间终点为150MPa时，mE值明显偏大，达到246.45GPa； 弹性模量选择区间的终点越接近拉伸强度，则mE值越接近自动杨氏模量的mE值。 当大于mE时，拉伸强度无法得到Rp0.2。

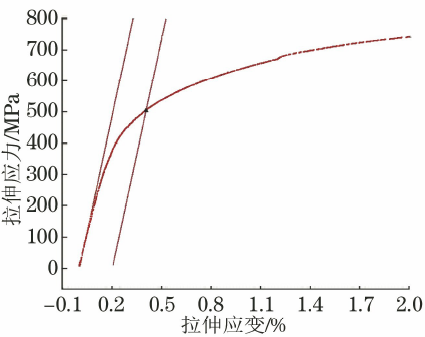
图7 DP780高强钢应力-应变曲线(选取杨氏模量30~150MPa)

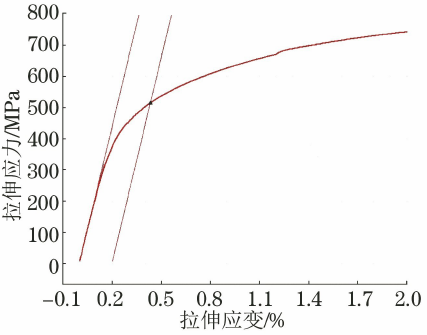
图8 DP780高强钢应力-应变曲线(选取杨氏模量30~300MPa)

图9 DP780高强钢应力-应变曲线(选取杨氏模量30~800MPa)

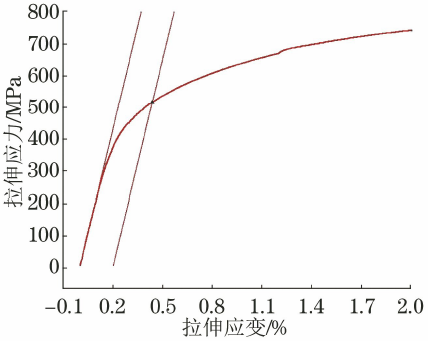
图10 DP780高强钢的应力应变曲线（自动杨氏模量）

从图7~图10可以看出，当弹性模量选择区间终点为150MPa时，弹性模量线与曲线弹性截面拟合程度较差，导致mE值明显偏大。 由于DP780高强钢的应力应变曲线呈现连续屈服现象，0.4%~0.5%应变值对应的应力值逐渐增大，因此mE值偏大，导致Rp0.2值小的。

综上所述

弹性模量线与应力应变曲线的拟合程度会影响弹性模量线的斜率mE的值，从而影响屈服强度Rp0.2的测量值。 对于拉伸曲线上有明显屈服平台的碳素结构钢，mE值对Rp0.2的测量值影响不大。 对于拉伸曲线上存在连续屈服现象的高强钢，mE值直接影响Rp0.2的测量值。

无论弹性模量如何选择，实验室均应检查拉伸试验后放大的应力-应变曲线，观察弹性模量线与曲线弹性截面的吻合程度。 如果贴合不好或引伸计处于弹性状态，出现段打滑的情况，应适当调整，直至贴合程度最佳，然后重新取值。

选自：《理化测试-物理卷》Vol.56 2020.4

作者：高晓勇，首钢京唐钢铁联合有限公司工程师